Research Article
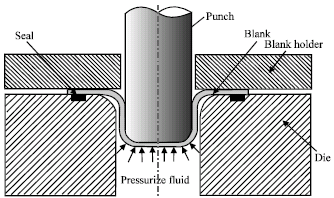
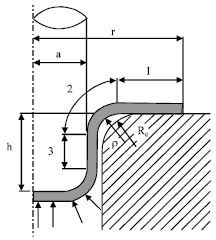
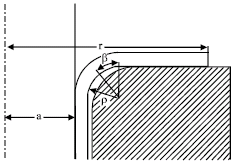
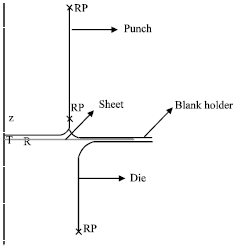
Theoretical Study and Finite Element Simulation of Tearing in Hydroforming Process
Faculty of Mechanical Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran
A. Shamsi
Faculty of Mechanical Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran
A. Gorji
Faculty of Mechanical Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran
S.J. Hosseinipour
Faculty of Mechanical Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran
M. Bakhshi-Jouybari
Faculty of Mechanical Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran