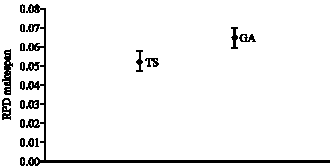
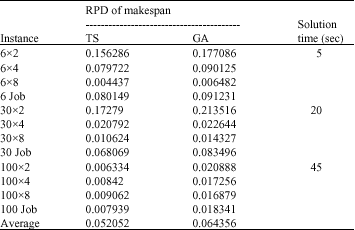
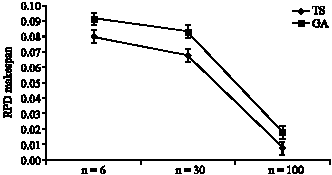
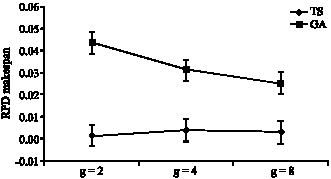
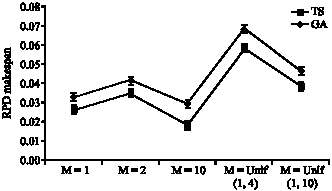
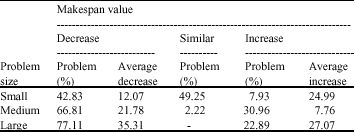
Research Article
A Tabu Search Approach to Hybrid Flow Shops Scheduling with Sequence-Dependent Setup Times
Department of Industrial Engineering, Mazandaran University of Science and Technology, Babol, Iran
M. Zandieh
Department of Industrial Management, Faculty of Management and Accounting, Shahid Beheshti University, G.C., Tehran, Iran
A. Alem-Tabriz
Department of Industrial Management, Faculty of Management and Accounting, Shahid Beheshti University, G.C., Tehran, Iran