Research Article
Efficiency Differences Across High Schools in Niğde, Province of Turkey
Department of Business Administration, University of Nigde, 51200, Nigde, Turkey
I. Torun
Department of Education, University of Nigde, 51200, Nigde, Turkey
This study examines the technical efficiency across high schools in Niğde Province of Turkey, using common methodology of Data Envelopment Analysis (DEA) and presents evidence on efficiency rankings of schools and possible efficiency improvements in educational institutions. The subject is obviously important, once it is recognized that a strong educational system is a driving force of economic prosperity in the face of highly competitive world markets and resources allocated to education are scarce. As shown in the recent literature on endogenous growth, a significant part of the long-run economic growth can be attributed to human capital accumulation which is closely related to the performance of educational institutions. In addition, considering the fact that budgetary conditions in most countries allow the transfer of only a limited amount of resources to education, it can be argued that those countries which use available resources in education efficiently will have higher human capital accumulation and hence higher long-run growth rates.
The efficient allocation of resources is especially important for developing countries, such as Turkey, in where resources are scarce, the rate of growth of population is high and therefore the share of funds allocated to education is inadequate to achieve satisfactory level of education. Departing from these observations, the Turkish government has launched restructuring program in public sector including educational institutions, which focused on achieving efficiency in public sector. It is apparent that the success of this reform is closely related to the empirical evidence provided on the measurement of efficiency in implementation, monitoring and evaluation stages of the program.
Although, there is fast growing literature on school efficiency in developed countries, studies on developing countries, including Turkey, are almost non-existent. In this study, we investigated the level of efficiency in high schools and reported on possible improvements to make inefficient schools efficient.
In recent years, public and professional interest in educational institutions has increased tremendously and schools are more and more the subject of analysis. A large number of empirical studies have already undertaken to measure inefficiencies in educational institutions employing the mathematical programming techniques. These studies focused on identifying efficient educational institutions which produce the highest levels of achievement given their inputs and compare them with inefficient institutions. This is evidently important because once inefficiencies in education are identified and quantified; policy can be constructed so as to maximize school achievements. In addition, the measurement of efficiency also provides valuable information for policy makers in implementing, monitoring and evaluating the reforms in education.
The empirical study on education economics is concentrated on the empirical analysis of the technical relationship between inputs and outputs of education. In this study, schools are considered as production units which turn educational inputs into educational outputs. Although, there is no consensus over the selection of input and output variables, those variables which are under the control of the educational institutions are in general, taken as the inputs of education production function such as the number of teachers and variables related to teaching environment and outputs are represented with exam scores (Worthington, 2001). One of the most cited and the oldest study on efficiency in education is carried out by Bessent et al. (1982). The present study attempted to determine technical efficiency levels of schools in Houston using the DEA analysis. Since then, a large number of empirical studies have investigated the efficiency in education in developed countries. Some of these studies are Jesson et al. (1987), Fare et al. (1989), Mancebon and Molinero (2000), Mancebon and Bandres (1999), Johnes (2006) and Waldo (2007).
Considering the fact that the exact form of the functional relationship between inputs and outputs is not known, some of the researchers in the study, stressed the importance of the assumed technology in the measurement of technical efficiency (Banker, 1984; Zhu and Shen, 1995; Engert, 1996; Pritchett and Filmer, 1999). In other words, the level of efficiency is closely related to the assumptions about the definition of technology. Fare et al. (1989), Duncombe et al. (1997), Bates (1997) Ray (1991), Engert (1996) and Ganley and Cubbin (1992) have employed both the constant returns and increasing returns technologies in their calculations of efficiency and found that the inefficiencies decrease when increasing returns technology is assumed implying the importance of scale economies in education.
Although, there is an extensive literature on efficiency in education for developed countries, the number of studies on developing countries is very limited. This is also a case for Turkey. To this best knowledge, there are only two studies investigated the level of efficiency in Turkish schools mainly for two reasons. The first one is related to the data restrictions and the second one is that the importance of efficiency in education has not been recognized yet in Turkey. One of these studies is undertaken by Baysal and Toklu (2001), in where the authors examine the level of efficiency for 11 high schools in Konya province. In this study, the number of teachers and salaries to personnel are used as input variables and the number of students won university entrance exams are used as output variables. The present study reports that only two of the 11 high schools are efficient and the level of efficiency ranges between 11.5 and 100% averaging 54%. In other words, providing that inefficient schools become efficient, it is possible to improve input usage about 46%.
In another study, Atan et al. (2002) found that schools in Ankara province differ significantly in terms of the level of efficiency. They measured efficiency for 22 Anatolian High Schools (a class of high schools offering quality education) using DEA analysis and data for 2001 using the number of students, teachers, classes, laboratories and computers as inputs and the number of graduates, pass university entrance exams as outputs. They reports that only 8 out of 22 Anatolian high schools are efficient and if inefficient schools become efficient, the outputs will increase about 21% with the available inputs.
Although, these studies provide some evidence on the level of efficiency in schools in Turkey, the coverage of schools employed in these studies is very limited and analysis is carried out using constant returns technology only. For this reason, we will investigate the technical efficiency of all high schools in Niğde Province assuming both constant returns and increasing returns technology in empirical educational production function.
Efficiency in education examines the ability of schools to turn the inputs of education into outputs. Given the production technology, if a school cannot reduce its inputs without causing a reduction in its outputs it is called efficient school. However, if a school achieves the current performance using higher number of inputs than other similar schools, this indicates that the school does not use its resources efficiently. These inefficiencies may be arising from mismanagement, inappropriate sizes of schools and external factors.
The main aim of the empirical studies on efficiency measurement is to construct empirical production frontiers to evaluate the performance across schools. Production frontier represents the highest possible performance that can be achieved using available technology. Each Decision Making Unit’s (DMU) efficiency, in this case a school, is measured by comparing the efficiency score of this unit with schools that constructs the frontier. Although, there are different alternative methods to determine production frontier (parametric and non-parametric), most of the previous empirical studies in education employed the DEA method.
Figure 1 provides a simple example of measuring efficiency using DEA and shows the meaning of efficiency.
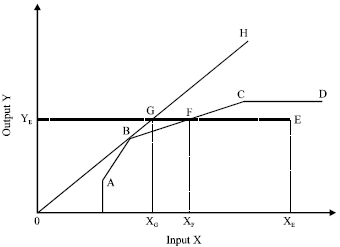 | |
| Fig. 1: | Efficiency frontier curve |
To simplify the presentation, it is assumed that schools use only one input to produce one output. In Fig. 1A-E represent schools in the input (X)-output (Y) plane. Under the assumption of constant returns to scale, the most efficient school is the one that has the highest output-input ratio in the case of one input and one output. In the figure, constant returns to scale is shown with a linear line stems from the origin. According to Fig. 1, the most efficient school is the school B since the slope of OH line has the highest value at point B. Thus, efficient production technology is determined by the OH line that goes through point B. All other points are inefficient because they are under this line.
After determining efficient frontier in this way, at the second stage, the efficiency scores for inefficient schools are calculated as follows. Assuming that the observation on the efficiency line (in present example this is shown by point B) is efficient, efficiency score corresponding to this point is one (or 100%). Schools which are under the efficiency line are inefficient and the level of inefficiency of these schools is related to the distance to line H. Efficiency score for school E, is determined by the ratio of XG/XE.
Although, it is easy to measure efficiency level for one input and one output, when the number of inputs and outputs are greater than one it becomes very difficult to measure efficiency scores. In such cases, the linear programming methods are employed to measure the efficiency scores. DEA model allows the measurement of efficiency when there are more than one input and output is developed by Charnes et al. (1978). DEA, is a non-parametric technique that is used in construction of empirical production frontier and evaluation of performances of homogenous DMU’s. In this analysis, DMU’s are schools which use more than one input to produce multiple outputs. In the analysis, assuming that the number of DMU’s is n and each of these units use m inputs and s output, the mathematical representation of DEA model can be written as (Lovell, 1993):
DEA model:
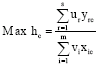 | (1) |
 |
where, c, represent the DMU that its efficiency level will be evaluated, yrj is the school j’s rth output, xij is school j’s ith input, ur and vi are the weights that will be obtained from solving the model corresponding to input r’s and output i’s, respectively. Model 1, involves the maximisation of objective function hc’s, DMU c’s weighted output to weighted inputs ratio, including itself under the restriction of no one DMU ratio is greater than one. The weights of ur and vi in the model is obtained with optimisation. To solve the optimisation problem given in model 1, we equate hc’s denominator to one thereby turning the problem into linear programming. Corresponding model suitable to linear programming can be written as:
(2) |
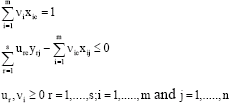 |
In model 2, it is assumed that constant returns technology is employed in the optimisation problem. In addition, as seen from the model 2, the weighted average of inputs is equal to one and outputs are maximised. This formulation of the DEA model is called input oriented efficiency measurement and indicates that schools try to minimise inputs given the outputs. The dual of the Primal Linear Programming Model given in model 2, can be written by defining the input weights of schools as θc and output weights as λj:
Dual model:
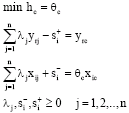 | (3) |
The values of θc scores obtained solving the model is equal to one and the slacks si+ and si¯ is equal to zero, school c is called efficient. The efficiency school implies that it is impossible for the school to achieve the given output level with using less inputs. If θc is smaller than one, these schools are called less efficient than the benchmark reference schools and the value of θc indicates the extent that school c needs to reduce input usage to reach efficient frontier. For inefficient schools reference schools are obtained using the optimum values of λj’s. To consider the Variable Returns to Scale (VRS) in the production, an extra restriction of
needs to be added to the model 3 (Banker et al., 1984).
Jackknifing method: As explained in the previous section, efficiency scores for schools are measured with the distance from the empirical production frontier. The empirical production frontier is determined by the schools which have the highest output level per inputs and efficiency scores for other schools are measured with respect to efficient schools. For this reason, it is very important for the reliability of results that the efficiency scores of those firms that constructs frontier are not outliers. This is because if the schools, which construct the frontier, are very different from the others in the province, when these schools are removed from the sample the efficiency level of the remaining schools will change. To determine whether outliers affects frontier and hence efficiency scores the Jackknifing method was employed. The other studies that employed jackknifing technique are as: Fare et al. (1989), Ray (1991), Ganley and Cubbin (1992), Bates (1997) and Engert (1996). Jackknifing method is a method that is used to test the consistency of the DEA results in case that a school with outlier observation is included in the analysis. Briefly, this method, involves measuring the efficiency scores by removing the reference schools one at a time from the DEA analysis and then testing changes in the efficiency rankings of schools and average efficiency values. To determine whether the efficiency rankings of schools change, the Spearman Rank Correlation coefficient is used and whether the average efficiency scores change when efficient schools dropped from the sample one at a time is tested using the F-test.
Data on inputs and outputs were collected for 35 high schools in Niğde during the 2004-2005 school years. The data is obtained mainly from Niğde Provincial Directorate for National Education and the Student Selection and Placement Centre (ÖSYM) publication of 2005 Student Selection Exam Results by Education Institutions. In the empirical analysis we employed three outputs and four inputs. The selection of the input and output variables is carried out in line with the existing empirical literature. Output variables involve students’ university exam scores on science (ÖSS-SAY), social science (ÖSS-SÖZ) and weighted average of Turkish and mathematics (ÖSS-EA). Input variables are the number of science teachers per student, the number of social science teachers per student, the number of classrooms per student and the number of laboratories per student.
Here, presents the empirical results of the study. In presenting DEA results, we measure and interpret efficiency scores assuming both constant returns to scale and variable returns to scale and assuming that output given so that the deviation of scores from one (or 100%) indicates savings possibilities in the use of inputs. Table 1 provides evidence on the stability of DEA results for efficient schools obtained from the Jackknifing method. The examination of the table shows that Spearman rank correlation coefficients ranges between 0.866 and 1.000 implying that the removal of efficient schools did not change the efficiency ranking of schools. It is also evident from the F-test results that once the efficient schools are dropped from the analysis the average efficiency scores do not show any statistically significantly difference.
| Table 1: | The stability of DEA results for efficient schools |
 | |
| *Shows that the null hypothesis of equal means could not be rejected at 1% level of significance | |
| Table 2: | Efficiency scores and savings possibilities in the use of inputs for high schools in Niğde (Assuming constant returns to scale) |
 | |
| Values in parenthesis indicates the number of times the efficient school became references to inefficient schools. Sct, Sst, Class, Lab are the inputs variables employed in the empirical analysis and represent the number of science teachers, social science teachers classes and laboratories per student, respectively | |
Taken together the evidence provided by both of the tests, it seems that the DEA results are consistent.
The results obtained from the DEA model given in Eq. 3 are provided in Table 2 and 3. Table 2 and 3 includes efficiency scores and potential improvements to achieve efficiency for inefficient schools. We calculated the inefficiency ratings for 35 high schools in Niğde Province of Turkey. An efficiency value of unity represents efficient performance indicating that the school is operating at a point on the frontier of the technology. Measures less than unity reflect the inefficient performance. Subtracting one from the measure yields the percent by which all inputs could be decreased proportionally given outputs and best practice technology. Mean efficiency estimated is equal to 0.617 assuming constant returns to scale implying that total inefficiency is about 38%.
| Table 3: | Efficiency scores and savings possibilities in the use of inputs for high schools in Niğde (Assuming variable returns to scale) |
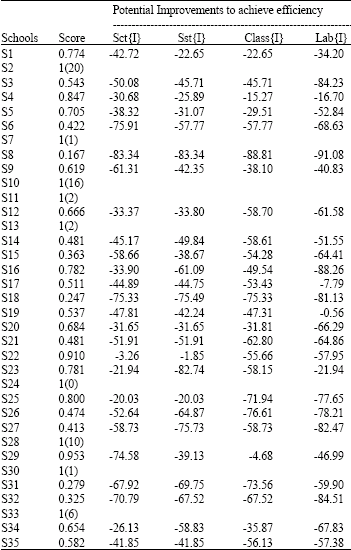 | |
| Values in parenthesis indicates the number of times the efficient school became references to inefficient schools. Sct, Sst, Class, Lab are the inputs variables employed in the empirical analysis and represent the number of science teachers, social science teachers classes and laboratories per student, respectively | |
The second column in Table 2 contains the efficiency measures for each school in the reference technology of constant returns to scale. Of the 35 schools, about 89 (31%) were found to be inefficient. The efficiency scores ranges from 0.165 to 1. The minimum efficiency score found was 16.5%. Only four of the 35 schools (schools 2, 10, 28, 33) were found efficient and these four schools appeared frequently in the reference set of inefficient schools. School 2 appeared 21 times, schools 10, 28, 33 appeared 17, 13, 10 times, respectively. Possible changes in inputs need to be undertaken to make inefficient schools as efficient is presented in the columns of 3 to 6 in Table 2. It is clear from Table 2 that inefficient schools uses too much inputs to achieve their level of output. For example, the least efficient school, school 8 employs almost 80% higher inputs to produce its output compared to the reference schools.
Table 3 provides the efficiency scores and potential improvements to achieve efficiency for inefficient schools assuming variable returns to scale technology in educational production function. As seen from the table, the number of efficient schools increased to nine. The calculated mean efficiency increased only slightly to 0.686 indicating the presence of about 31% inefficiency in input usage in education. The examination of the second column in Table 3 shows that only about 26 (9%) of the schools are efficient and the efficiency scores ranges from 0.167 to 1. The schools that were found efficient assuming constant returns are found to be efficient using variable returns technology and they still appeared frequently in the reference set of inefficient schools. This finding is consistent with the findings of the earlier studies of Fare et al. (1989), Duncombe et al. (1997), Bates (1997) Ray (1991), Engert (1996) and Gonley and Cubbin (1992) which shows that the inefficiencies decrease when increasing returns technology is assumed implying the importance of scale economies in education.
In this study, we investigated the technical efficiency across high schools in Niğde and provided evidence on potential improvements to achieve efficiency for inefficient schools. The results imply that all these schools appear to have had adequate resources, if fully utilized. When we employed constant returns technology, the total inefficiency is about 38% and out of the 35 schools, about 89 (31%) were found to be inefficient. The corresponding values are 31%, 74 (26%) under variable returns to scale technology. These values indicate that schools differ significantly in terms of inefficiencies in input usage and if they began to utilize their resources fully they would be able to increase their achievement about 35 %. In addition, the results have shown that the number of efficient schools has increased when variable returns technology is employed without affecting the efficiency scores of highly inefficient schools. This also indicates that scale economies are important in education and the use of increasing returns technology in education production function is more appropriate. These findings also show the importance of applied studies on the subject for policy purposes. Identification and quantification of inefficiencies will definitely provide valuable information for policy makers in their efforts to construct, monitor and evaluate the policies aimed to maximize school achievement.