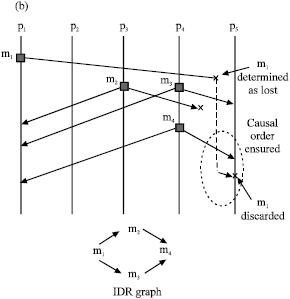
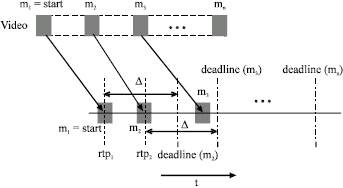
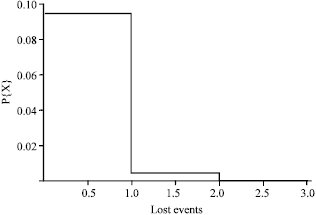
Research Article
An Efficient Δ-Causal Algorithm for Real-Time Distributed Systems
Department of Computer Science, National Institute of Astrophysics, Optics and Electronics, Luis Enrique Erro No. 1, 72840, Tonantzintla, Puebla, Mexico
E. Lopez Dominguez
Department of Computer Science, National Institute of Astrophysics, Optics and Electronics, Luis Enrique Erro No. 1, 72840, Tonantzintla, Puebla, Mexico
G. Rodriguez Gomez
Department of Computer Science, National Institute of Astrophysics, Optics and Electronics, Luis Enrique Erro No. 1, 72840, Tonantzintla, Puebla, Mexico
J. Fanchon
Universite de Toulouse, LAAS-CNRS, 7 Ave. Colonel Roche, 31077 Toulouse Cedex, France