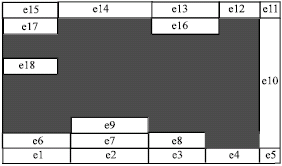
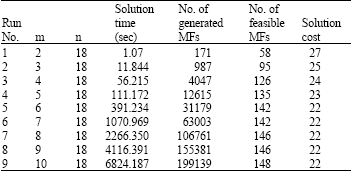
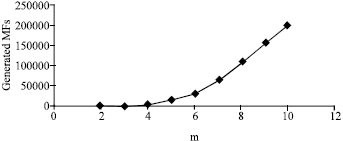
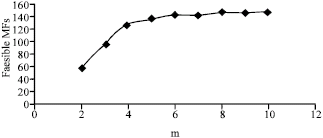
Research Article
A Volume Decomposition Model to Determine Machining Features for Prismatic Parts
Department of Industrial Engineering, Sharif University of Technology, Tehran, Iran
D.M. Imani
Department of Industrial Engineering, Sharif University of Technology, Tehran, Iran