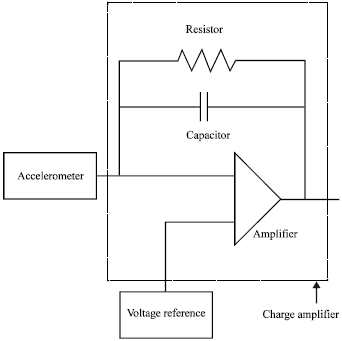
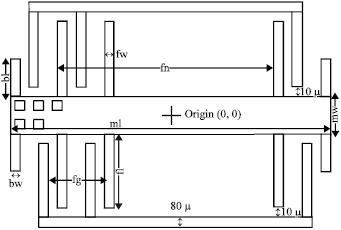
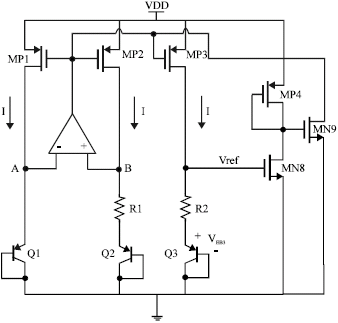
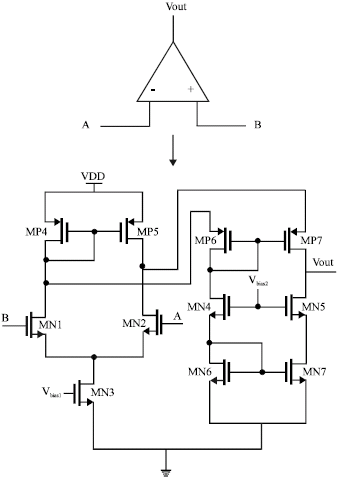
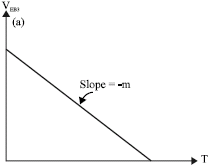
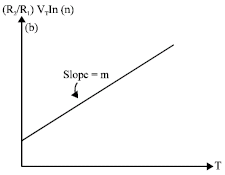
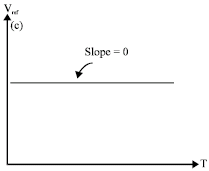
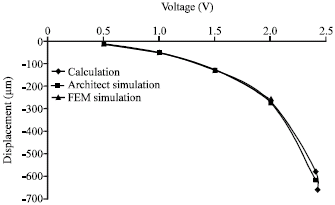
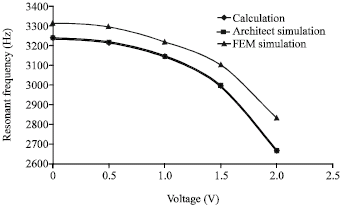
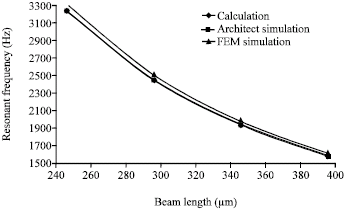
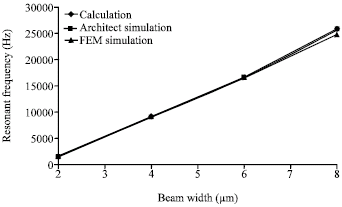
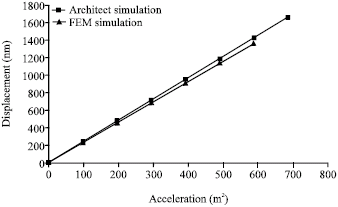
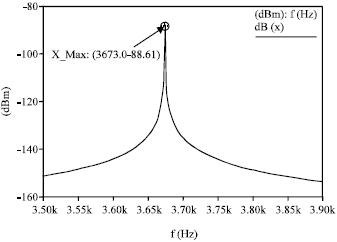
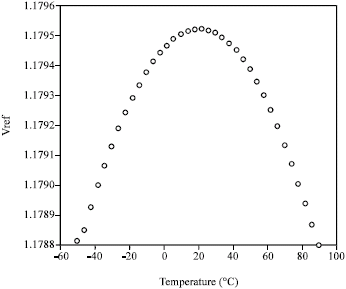
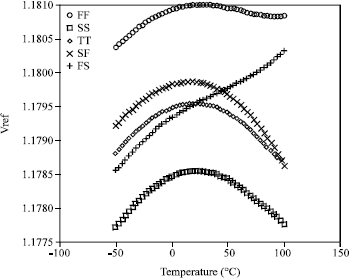
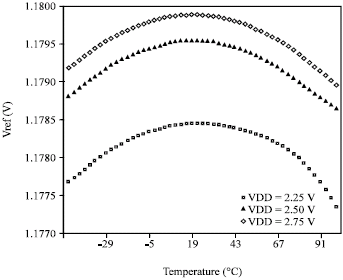
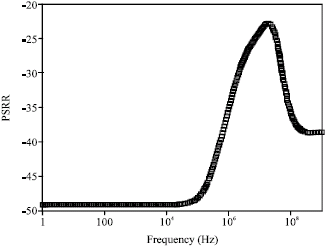
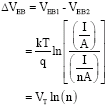Research Article
Analysis of Capacitive Microelectromechanical System Accelerometer Proposed with Voltage Reference in Read-Out Circuit
Engineering Campus, Collaborative Microelectronic Design Excellence Centre, Universiti Sains Malaysia, 14300 Nibong Tebal, Sri Ampangan, Pulau Pinang, Malaysia
O. Sidek
Engineering Campus, Collaborative Microelectronic Design Excellence Centre, Universiti Sains Malaysia, 14300 Nibong Tebal, Sri Ampangan, Pulau Pinang, Malaysia
A.Z. Ruhaifi
Engineering Campus, Collaborative Microelectronic Design Excellence Centre, Universiti Sains Malaysia, 14300 Nibong Tebal, Sri Ampangan, Pulau Pinang, Malaysia