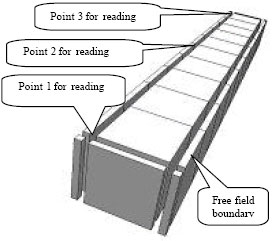
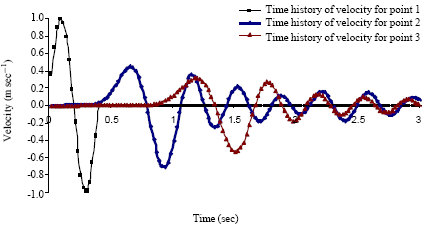
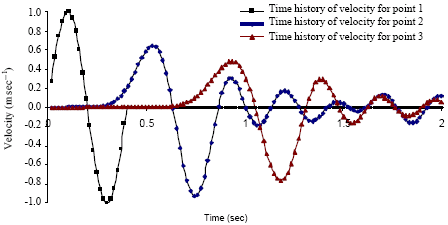
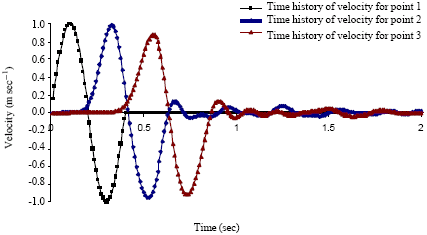
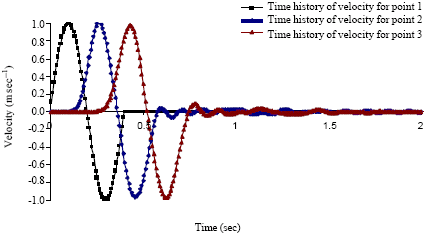
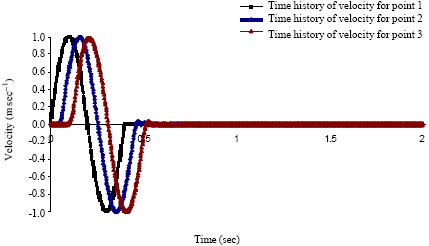
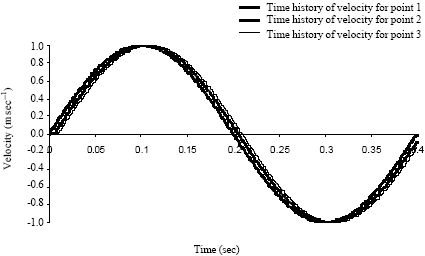
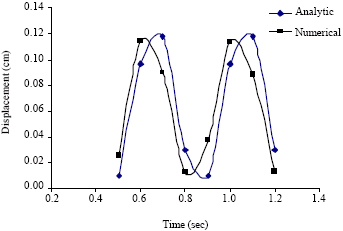
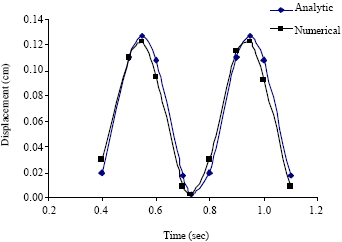
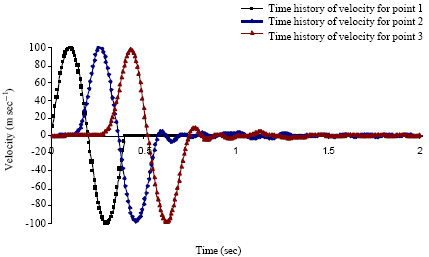
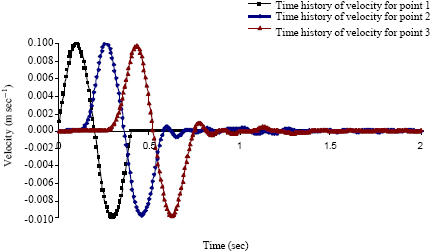
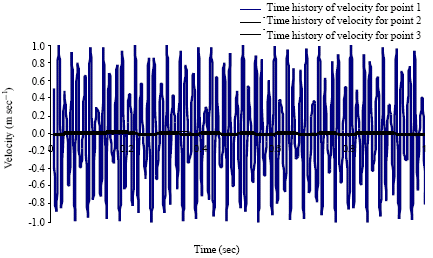
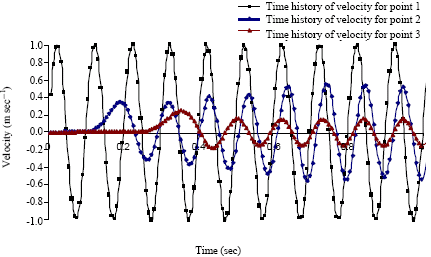
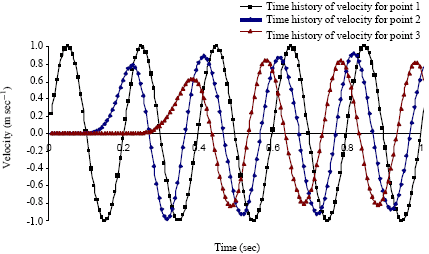
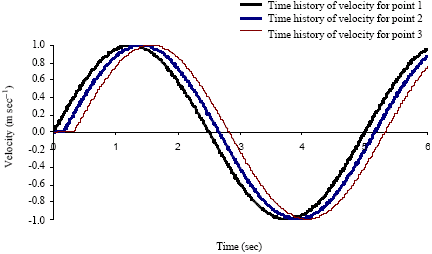
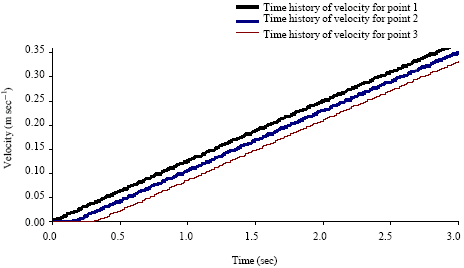
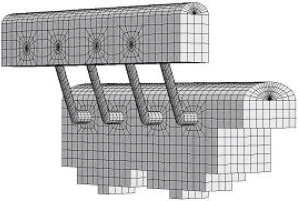
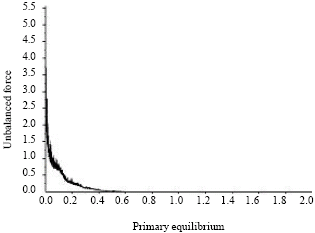
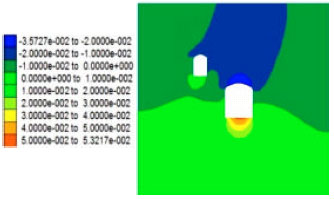
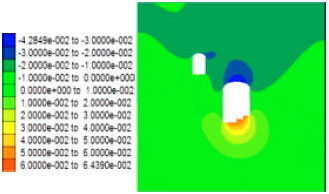
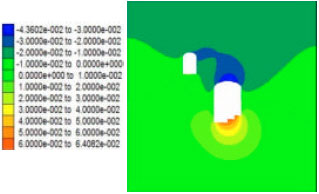
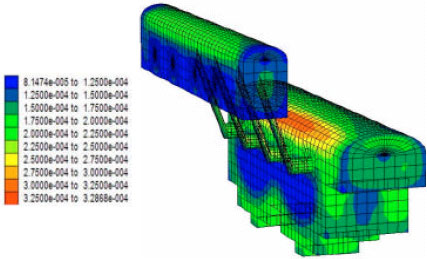
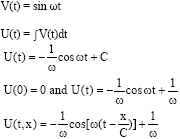Case Study
Seismic Analysis of Underground Spaces to Propagation of Seismic Waves (Case Study: Masjed Soleiman Dam Cavern)
Faculty of Mining Engineering, Sahand University of Technology, Iran
K. Goshtasbi
Department of Mining Engineering, Tarbiat Modares University, Iran
H. Aghababaei
Faculty of Mining Engineering, Sahand University of Technology, Iran
N. Khaji
Department of Civil Engineering, Tarbiat Modares University, Tehran, Iran
H. Merzai
Faculty of Mining Engineering, Shahrood University of Technology, Iran