Research Article
Poultry Feed Brands Selection Using Profile Analysis
Department of Statistics, Imo State University, Owerri, Imo State, Nigeria
F.N. Nwobi
Department of Statistics, Imo State University, Owerri, Imo State, Nigeria
In poultry farming, the production of high quality (healthy and weighty) birds is always desired, as this boosts the revenue of the poultry farmer. To ensure this, the best of inputs (especially, poultry feeds) has to be used on the birds. This study is set out to show how profile analysis could be carried out and particularly, its application in the selection of poultry feed brands.
Profile analysis, according to Ott (1999), is a specific style of Multivariate Analysis of Variance (MANOVA). It is equivalent to repeated measures MANOVA (Tabacknick and Fidell, 2006), because of its multiple responses taken in sequence on the same subject(s). Usually, the responses are taken over time as in weekly weight measurements to establish growth curves (Littell et al., 1998).
THEORY AND PROCEDURE OF PROFILE ANALYSIS
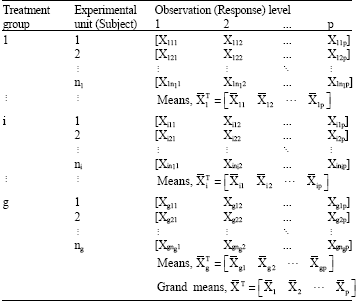
Let Xijk, i = 1, 2, …, g; j = 1, 2, …, ni; k = 1, 2, …, p, be an observation (a response) in a repeated measures experiment, where, i, j and k stand for treatment group (population), selected subject in the i-th treatment group and observation (response) level, respectively.
Let,
(1) |
denote the response vector for the j-th subject within the i-th treatment group and denote the mean response vector for the ith treatment group.
(2) |
Multivariate Analysis of Variance (MANOVA) is the natural choice for analyzing the type of data in the one-way completely randomized design described in Table 1, since it models the interdependencies among the response variables. However, profile analysis (Repeated Measures MANOVA) is most appropriate.
MANOVA with repeated measures is used when the measure that is repeated (e.g., across time) is a compound formed in the usual MANOVA fashion across multiple dependent variables. Thus, it is different from having multiple repeated measures factors (Tabacknick and Fidell, 2006).
It is worthy of note that certain assumptions and conditions Morrison (2002) and Tabacknick and Fidell (2006) must be met before profile analysis could be carried out on any set of data.
| Table 1: | Layout of Repeated Measures Design for g-Group Profile Analysis |
 | |
The question of equality of the population mean response vectors sought in MANOVA which is given by:
H0 : μ1 = μ2 = … = μg |
is divided into several specific possibilities. The question is formulated in a stage-wise fashion:
| • | Are the profiles parallel? Or equivalently: H01: μ1k-μ1(k-1) = μ2k-μ2(k-1) = … = μgk -μg(k-1); k = 2, 3, …, p |
| • | Assuming the profiles are parallel, are they coincident? Or equivalently: H02 :μ1k = μ2k = … = μgk; k = 1, 2, …, p |
| • | Assuming the profiles are coincident, are they level? That is, are all means equal to the same constant? Or equivalently: H03: μ11 = μ12 = … = μ1p = μ21 = μ22 = … = μ2p = … = μg1 =μg2 = … = μgp |
Before testing the hypothesis of parallelism, it is advisable to make a plot of the means (otherwise known as average profiles).
Test for parallel profiles: This test is achieved by working with the successive differences in the responses. The profiles are parallel if the differences are the same across the treatment groups. Thus, the null hypothesis in stage 1 can be written as:
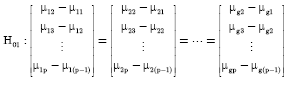 |
or
H01: Cμ1 = Cμ2 = … = Cμg |
where, C is contrast matrix given by:
 | (3) |
For independent samples of sizes, n1, n2, …, ng from the g-groups, H01 can be tested (in the usual one-way MANOVA fashion) by constructing the contrast-transformed observation vectors:
CXij; i = 1, 2, …, g; j = 1, 2, …, ni |
having sample mean vectors:
C |
and grand mean vector, C![]()
There are several different multivariate test statistics available for the test of parallel profile, all of which will generally yield equivalent results. Amongst the four common test statistics-namely Wilks Lambda, Pillai’s Trace, Hotelling-Lawley Trace and Roy’s Greatest Root; Wilks Lambda (Λ) is the most desirable because it can be converted exactly to an F-statistic (Ott, 1999; Everitt and Dunn, 2001). For details of this conversion and the exact distribution of Λ, see Johnson and Wichern (2001). It also presented a modification of Λ due to Bartlett (1938) for cases where the number of groups is more than three (g>3), as well as when large sample sizes are involved. It is worthy of note here that (p-1) would replace p in the circumstances above.
Employing the Wilks lambda criterion, therefore, H01 is rejected at α level if the ratio of generalized variances:
(4) |
is too small, or rather still if its equivalent F-statistic is greater than the critical value. For instance, where (p-1)≥1 and g = 3, the critical region would be:
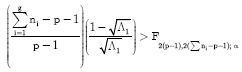 | (5) |
The matrices B1 and W1 in Eq. 4 are the treatment (Between) sum of squares and cross products, respectively and residual (Within) sum of squares and cross products for the CXij’s given as:
(6) |
and
(7) |
If H01 is rejected, it would be concluded that at least one of the average profiles is significantly different. Consequently, it would rather be unreasonable to embark
on testing the second null hypothesis. Otherwise proceed with the test.
Test for coincident profiles: The second null hypothesis investigates whether the profiles are superimposed on one another or rather identical. Under the condition of parallel profiles will be coincident only if the total heights:
are equal (Johnson and Wichern, 2001). Therefore, the null hypothesis at this stage can be written in the equivalent form:
H02: 1Tμ1 = 1Tμ2 = … = 1Tμg |
Where:
(8) |
Hence, the test is univariate, based on the univariate observations:
1TXij, i = 1, 2, … , g; j = 1, 2, … , ni |
Invariably, this is equivalent to performing a one-way ANOVA on the subject totals. Timm (1975) stated that the univariate and multivariate tests are equivalent, assuming parallelism. Nevertheless, the multivariate test approach is preferable since the data have already been arranged in a multivariate configuration for the first test.
Employing the Wilks lambda criterion, H02 is rejected at α level if the ratio of generalized variances:
(9) |
is too small, or rather still if its equivalent F-statistic is greater than the critical value. Generally, the critical region for the null hypothesis of coincident profiles is given by:
 | (10) |
unless where a modification of Λ2 due to Bartlett is, however, sought.
The matrices B2 and W2 in Eq. 9 are, respectively given as:
(11) |
and
(12) |
If H02 is rejected, it would be concluded that the profiles were not identical and embarking on testing the third null hypothesis would rather be unreasonable. Otherwise, proceed with the test.
Test for level profiles: The third null hypothesis investigates whether all variables have the same mean, so that the common profile is level. That is, μ1 = μ2 = … = μp.
A simple way to approach this problem is to again take successive differences, as was done in the first test. If the profile is indeed level, then the (p-1) differences should be zero. Thus, the null hypothesis at this stage can be written as:
H03 = Cμ = 0 |
where, C is as given by Eq. 3 and μ (the common mean vector) is estimated by ![]() (the sample grand mean vector).
(the sample grand mean vector).
Employing Wilks Lambda criterion, as before, H03 is rejected at α level if the ratio of generalized variances:
(13) |
is too small, or rather still if its equivalent F-statistic is greater than the critical value. Generally, the critical region for the null hypothesis of level profiles is given by Ott (1999) as:
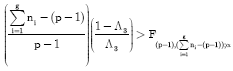 | (14) |
The matrix W3 in Eq. 13 is the same as W1 in Eq. 7, while under H03 the between sum of squares and cross-products for the CXij’s is:
| (15) |
If H03 is rejected, the conclusion thus becomes that all the means are not equal to the same constant. Otherwise, the profiles are level.
Contrasts following profile analysis: The major description of result in profile analysis, especially whenever the parallelism or levels hypothesis is rejected, is typically the plot of average profiles. However, when there are more than two levels of significant effects in profile analysis (in MANOVA, generally), it is often desirable to perform contrasts (example, Dunnett’s, Tukey, Bonferroni, or Scheffe’) to pinpoint sources of variability (Tabacknick and Fidell, 2006).
A practical example is presented on the application of profile analysis in analyzing the performances of three brands of poultry feed with a view to selecting the best brand.
Data collection and description: The data for this study were collected from the Planning, Research and Statistics Unit of Talented Royal Apex Project (TRAP), Owerri, Imo State of Nigeria. The data were the outcome of an experiment conducted to study the resultant weight-yields of poultry birds upon consumption of three brands of poultry feed in Ndubuisi Farms (a subsidiary of TRAP), with a view to comparing a locally-produced brand of poultry feed by TRAP (branded TRAP FEEDS) with two other brands (GUINEA FEEDS and TOP FEEDS).
Thirty day-old male turkey broilers were randomly selected from a batch of fifty-with common features-and put in three different poultry houses (ten in each). The birds were properly identified (by numbers) and weighed (in grammes). TOP, GUINEA and TRAP FEEDS were equitably administered to the birds in poultry houses 1, 2 and 3, respectively, for the eight-week period. Also, conventional feeding and health programmes obtainable in poultry farming were strictly observed.
Analysis: The data were analyzed by employing the profile analysis procedure outlined earlier. First, as tradition demands, the data were checked and it is sufficient to say that all the assumptions of profile analysis were satisfied. Although there were less than 20 birds in each of the treatment groups (purposely done to avoid over-crowding in the poultry houses), with equal sample sizes (n1 = n2 = n3) and n1>p; i = 1, 2 and 3, the multivariate normality assumption is not likely to be violated. Besides, profile analysis is as robust to violation of multivariate normality assumption as other forms of MANOVA (Tabacknick and Fidell, 2006).
A plot of the average profiles for the weight-yields of the birds in the three treatment groups is constructed (Fig. 1) and then followed by the test for parallel profiles.
 | |
| Fig. 1: | Average profiles of week-specific weights poultry birde for three brands of feeds |
Testing for parallel profiles: We have the hypothesis of parallelism as:
H01 : Cμ1 = Cμ2 = Cμ3 |
By using Eq. 6
 |
and Eq. 7
 |
Equation 4 yields Λ1 = 2.733E-3 (using MATLAB 6.0), while with p = 8 and g = 3, Eq. 5 yields:
Consequently, H01 is rejected at the 5% level of significance.
The result of the analysis showed that the profiles were not parallel and this caused the other two hypotheses (H02 and H03) contingent on the tenability of H01, not to be tested. In other words, significant differences existed amongst the profiles of the three treatment groups.
For profile analysis, the major description of results is typically a plot of profiles. Figure 1 showed that the average profile for TRAP FEEDS (Group 3) was well above the other two groups and this implied that its average performance was the highest regarding the resultant weekly weight-yields of the birds upon consumption.
Furthermore, contrasts performed by the method of Scheffe’ showed that there was no significant difference between the profiles of TOP and GUINEA FEEDS while the profile of TRAP FEEDS was significantly different from those of TOP and GUINEA FEEDS.
Consequently, TRAP FEEDS was selected as the best brand of poultry feed amongst the three brands used in the farm.
In this study, we have presented the procedure of carrying out profile analysis-the most appropriate statistical method for analyzing repeated measures data. We have also demonstrated the application of profile analysis in analyzing the performances of three brands of poultry feed, to know whether they are equal. The analyses showed that the profiles were not parallel (that is, statistically significant differences exist in the average performances of the feeds). The average profile of TRAP FEEDS was found to be well above those of the other two brands of feed, which implied highest performance. Hence, TRAP FEEDS was selected as the best brand of poultry feed for the birds in the farm.
Chijioke Samuel Chimuanya Reply
This is a good work,we really appreciate the authors more grace!