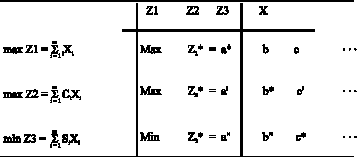
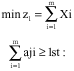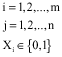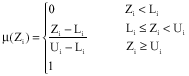Research Article
Developing and Solving a New Model for the Location Problems: Fuzzy-Goal Programming Approach
Department of Industrial Management, Allame Tabatabaee University, Tehran, Iran
A. Kazemi
Department of Industrial Engineering, Islamic Azad University of Qazvin, Qazvin, Iran
J.S. Sadaghiani
Department of Industrial Management, Allame Tabatabaee University, Tehran, Iran
A. Yaghoubi
Department of Industrial Engineering, Islamic Azad University of Qazvin, Qazvin, Iran
H. Mashatzadegan
Department of Industrial Engineering, Islamic Azad University of Qazvin, Qazvin, Iran