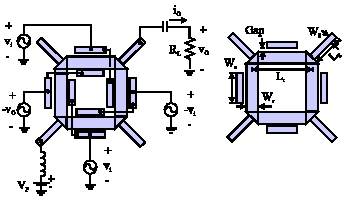
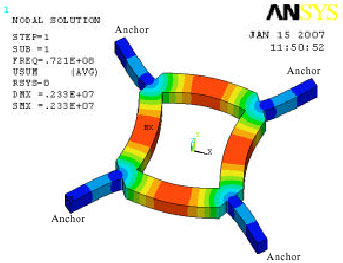
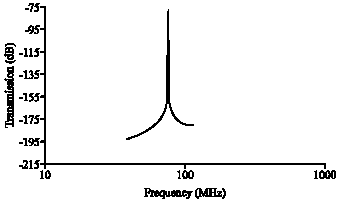
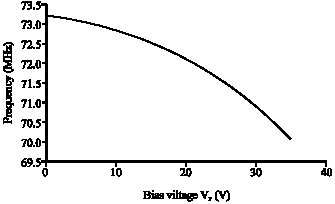
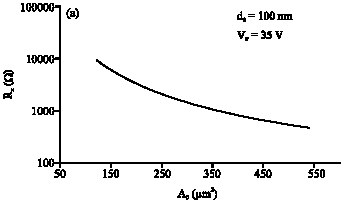
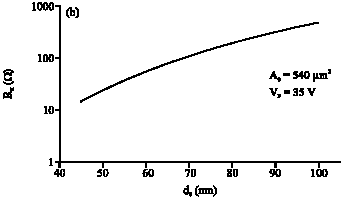
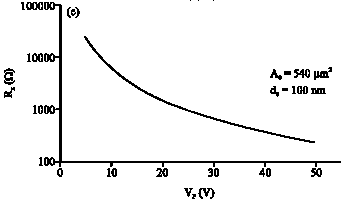
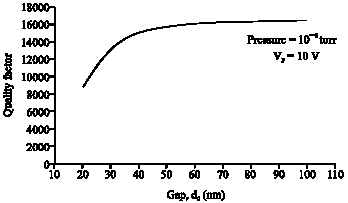
Research Article
Comprehensive Analysis of a High-Q, Low Motional Resistance, Very High Frequency MEMS Resonator
Department of Electrical Engineering,
S.H. Keshmiri
Departments of Electrical Engineering and Physics, Faculty of Engineering, Ferdowsi University, Mashhad, 91775-1111, Iran