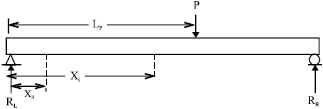
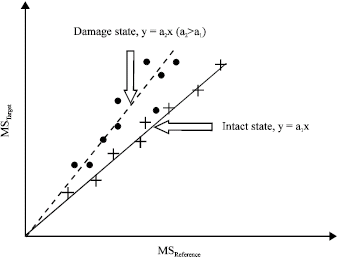
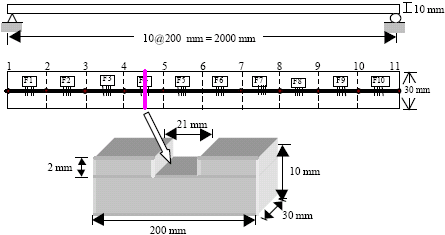
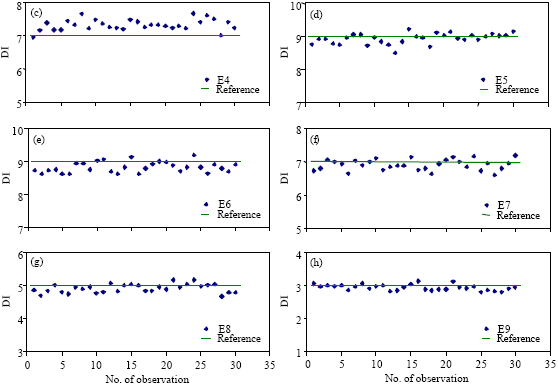
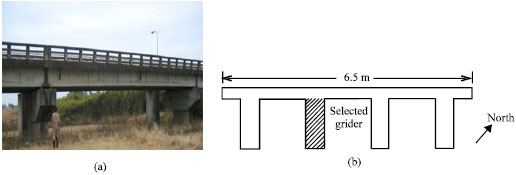
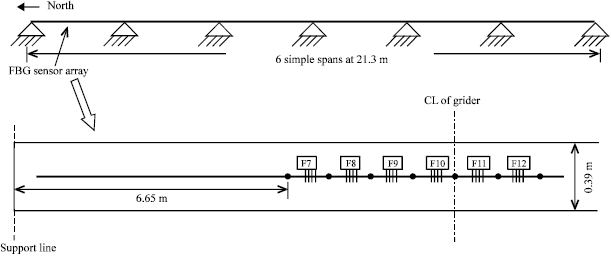
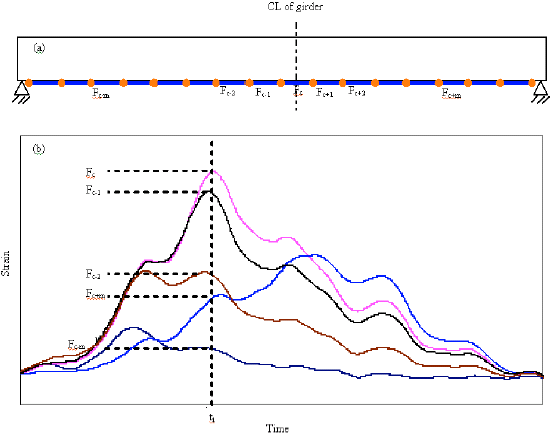
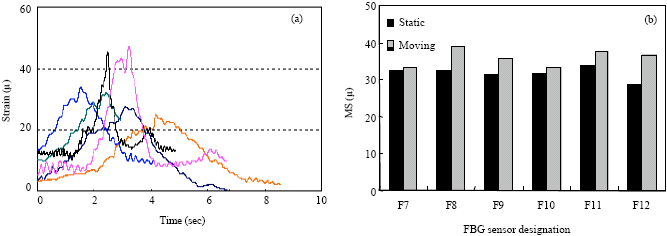
Research Article
Structural Health Monitoring Using Distributed Macro-Strain Response
Department of Urban and Civil Engineering, Ibaraki University, 4-12-1, Naka Narusawa, Hitachi, Ibaraki, 316-8511, Japan
Z.S. Wu
Department of Urban and Civil Engineering, Ibaraki University, 4-12-1, Naka Narusawa, Hitachi, Ibaraki, 316-8511, Japan