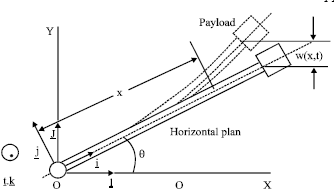
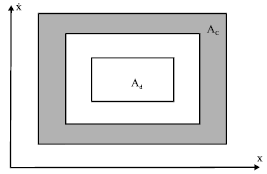
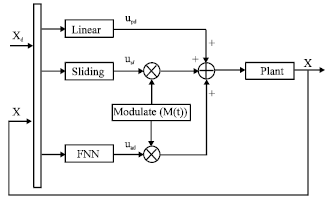
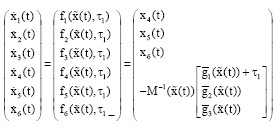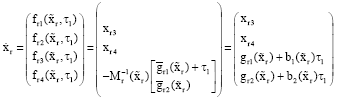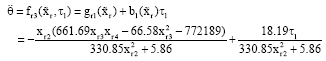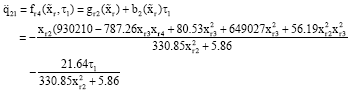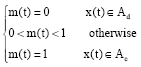Research Article
Stable Direct Adaptive Control as Nonlinear Hybrid Controller for Flexible Manipulator
Islamic Azad University, Arak Branch, Astaneh Campus, Astaneh, Iran
M. Teshnehlab
K.N. Toosi University, Seyyed Khandan, Shariati Street, Tehran, Iran
M. Aliyari Sh
K.N. Toosi University, Seyyed Khandan, Shariati Street, Tehran, Iran
M. Aliasghary
Istanbul Technical University, Istanbul, Turkey