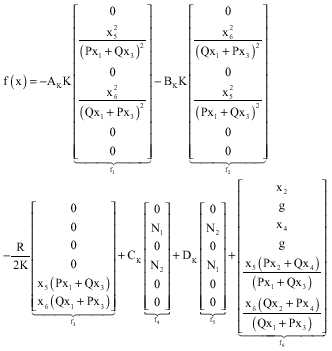
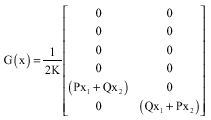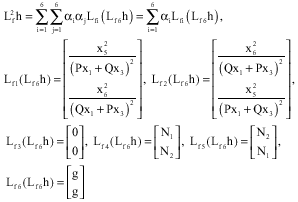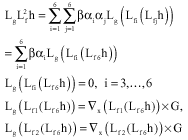Research Article
Adaptive Control of a Double-Electromagnet Suspension System
Faculty of Electrical Engineering, Amirkabir University of Technology, Tehran, Iran
A.R. Yazdizadeh
Faculty of Electrical Engineering, Power and Water University of Technology, Tehran, Iran
H.A. Talebi
Faculty of Electrical Engineering, Amirkabir University of Technology, Tehran, Iran
H. Eliasi
Faculty of Electrical Engineering, Amirkabir University of Technology, Tehran, Iran