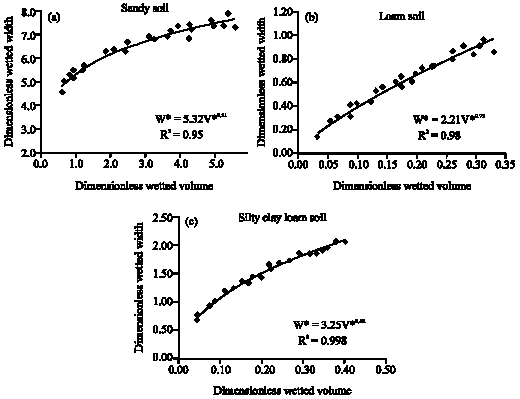
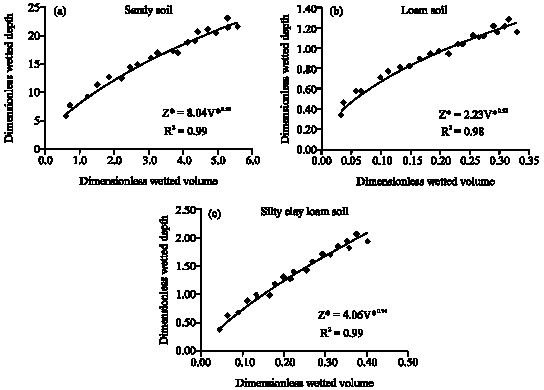
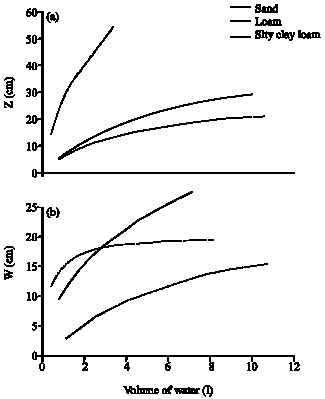
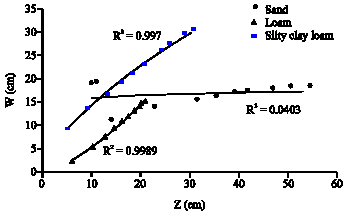
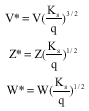Research Article
Simulation of Soil Wetting Pattern Under Point Source Trickle Irrigation
Department of Irrigation and Drainage
S. Boroomand-Nasab
Faculty of Water Engineering, Shahid Chamran University, Ahwaz, Iran
M. Behzad
Faculty of Water Engineering, Shahid Chamran University, Ahwaz, Iran