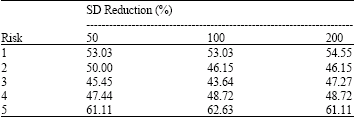
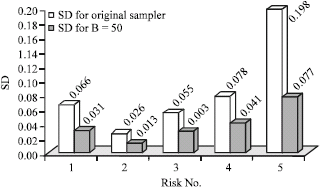
Research Article
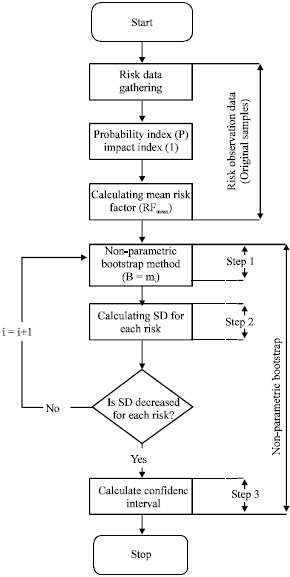
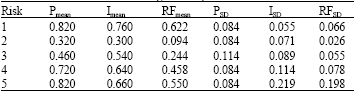
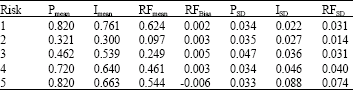
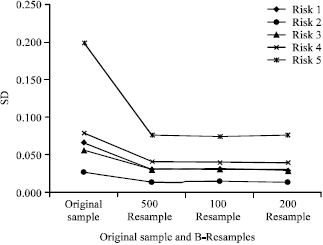
A Non-Parametric Statistical Approach for Analyzing Risk Factor Data in Risk Management Process
Department of Industrial Engineering, Graduate School, Islamic Azad University, South Tehran Branch, Member of Young Researchers Club, No. 209, North Iranshahr Street, P.O. Box 11365/4435, Tehran, Iran
S.M. Mousavi
Department of Industrial Engineering, Graduate School, Islamic Azad University, South Tehran Branch, Member of Young Researchers Club, No. 209, North Iranshahr Street, P.O. Box 11365/4435, Tehran, Iran
A. Aminian
Department of Industrial Engineering, Islamic Azad University, Gachsaran Branch, P.O. Box 1694913445, Gachsaran, Iran