Research Article
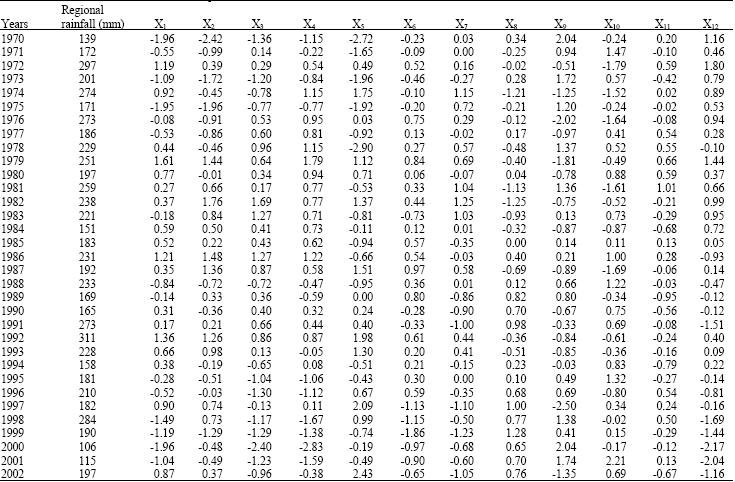
Seasonal Rainfall Forecasting Using Artificial Neural Network
Department of Climatology, Isfahan University and Researcher of Climatological Research Institute, Mashhad, Iran
M. Mousavi-Baygi
Department of Water Engineering, Faculty of Agriculture, Ferdowsi University of Mashhad, Iran
M. Habibi-Nokhandan
Atmospheric Science and Meteorological Research Center (ASMERC), Director of Climatologically Research Institute (CRI), Mashhad, Iran