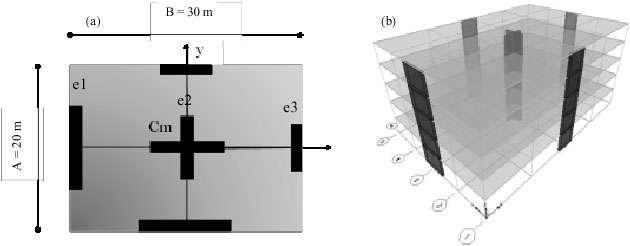
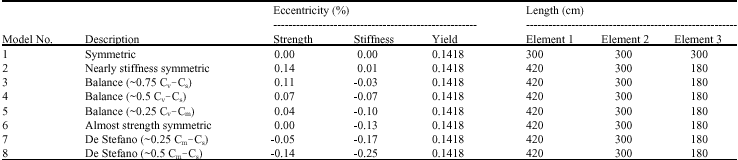
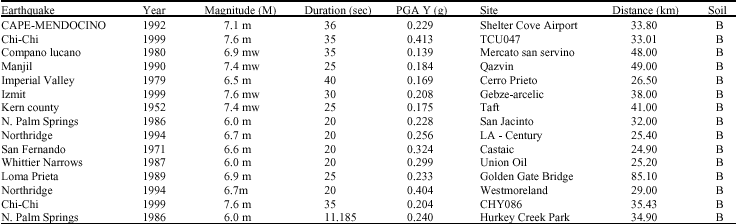
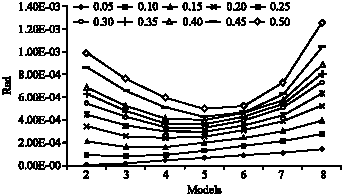
Research Article
Performance of Asymmetric Multistory Shear Buildings with Different Strength Distributions
International Institute of Earthquake Engineering and Seismology, P.O. Box 19395-3913, Tehran, Iran
A.S. Moghadam
Structural Engineering Research Center, International Institute of Earthquake Engineering and Seismology, Tehran, Iran