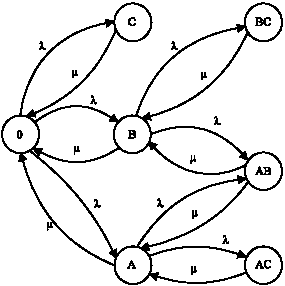
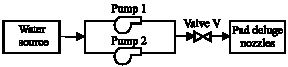
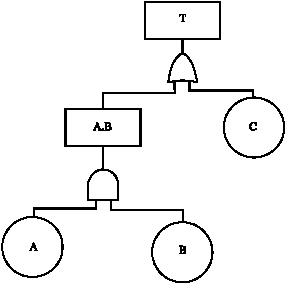
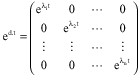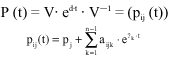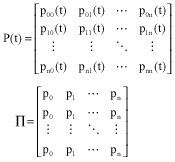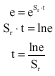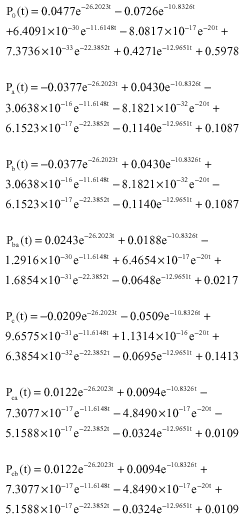Research Article
A Methodology for Analyzing the Transient Availability and Survivability of a System with Every Combination of Components by Using Fault Tree
Department of Industrial Management, Allameh Tabatabaee University, Tehran, Iran
Farhad Ghassemi-Tari
Department of Industrial Engineering, Sharif University of Technology, Tehran, Iran
Mohsen Rahimi Mazrae Shahi
Department of Industrial Management, Allameh Tabatabaee University, Tehran, Iran
Jamshid Salehi Sadaghiani
Department of Industrial Management, Allameh Tabatabaee University, Tehran, Iran
Ali Mahtasshami
Department of Industrial Management, Allameh Tabatabaee University, Tehran, Iran