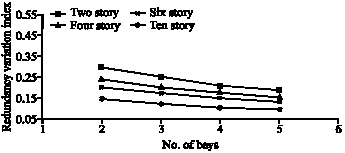
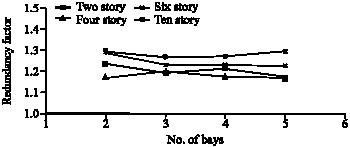
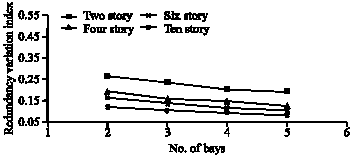
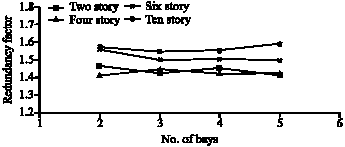
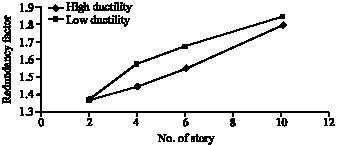
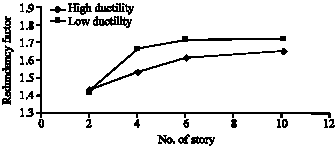
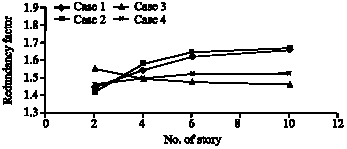
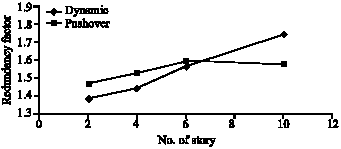
Research Article
A Nonlinear Dynamic Based Redundancy Index For Reinforced Concrete Frames
Science and Research Branch, Islamic Azad University, Tehran, Iran
A.S. Moghadam
Department of Civil Engineering, International Institute of Earthquake Engineering and Seismology, Tehran, Iran
A. Massumi
Department of Civil Engineering, Graduate School of Engineering, Tarbiat Moallem University of Tehran (Kharazmi), Tehran, Iran