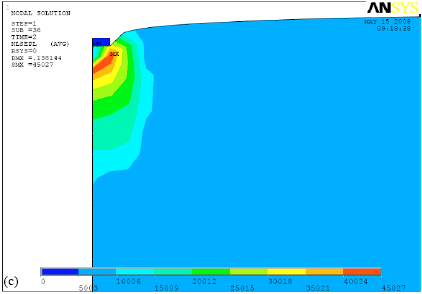
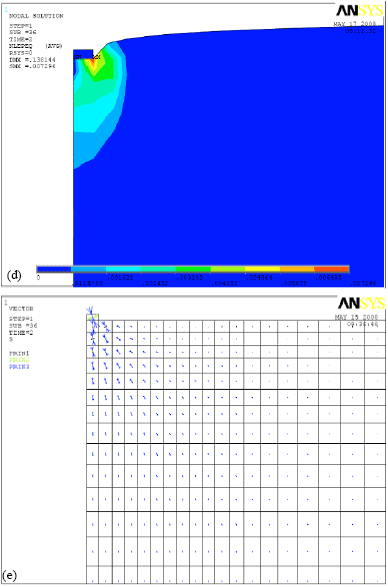
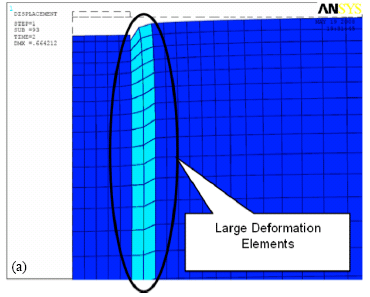
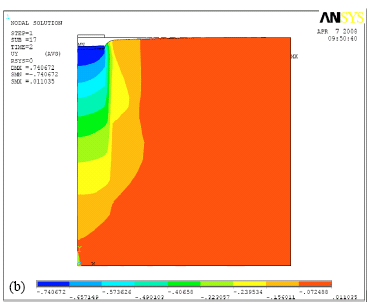
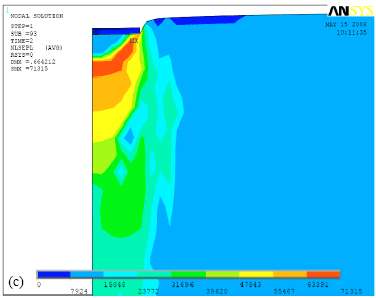
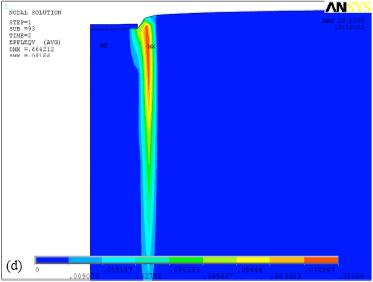
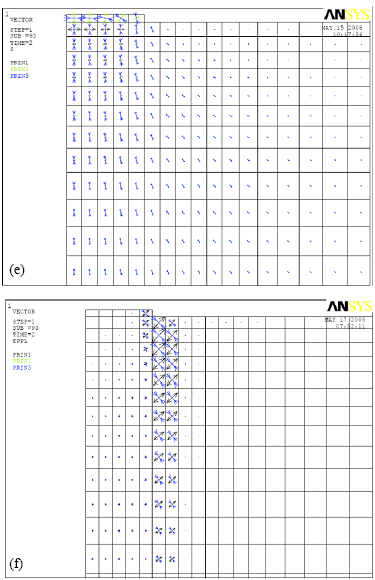
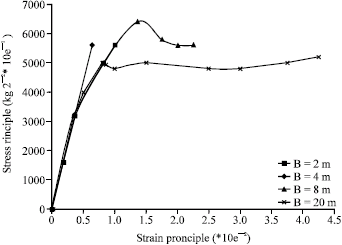
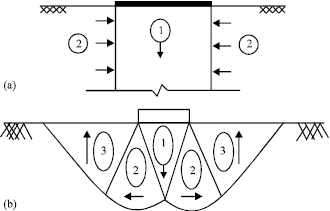
Research Article
Numerical Analysis of Interaction Between Earth and Large Foundations Regarding Size Effect
Department of Civil Engineering, Amirkabir University of Technology, (Tehran Polytechnic) -424, Hafez Avenue, Tehran, Iran
S.A. Amirshahkarami
Department of Civil Engineering, Amirkabir University of Technology, (Tehran Polytechnic) -424, Hafez Avenue, Tehran, Iran