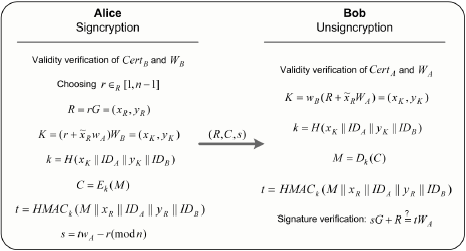
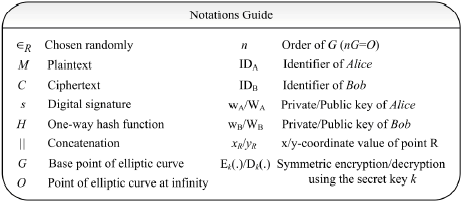
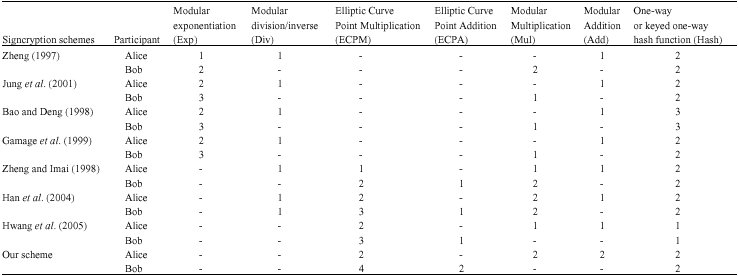
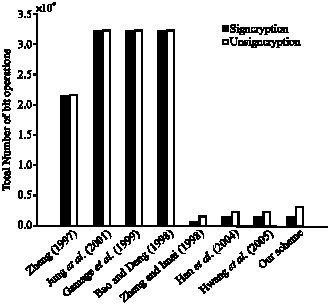
Research Article
An Elliptic Curve-Based Signcryption Scheme with Forward Secrecy
School of Electrical Engineering, Iran University of Science and Technology, Postal Code 16846-13114, Tehran, Iran
Ali Asghar Beheshti Shirazi
School of Electrical Engineering, Iran University of Science and Technology, Postal Code 16846-13114, Tehran, Iran