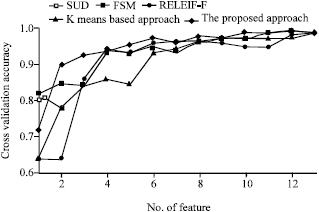
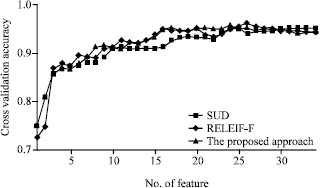
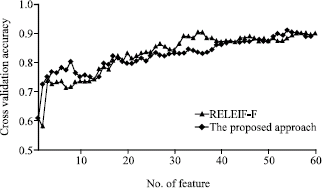
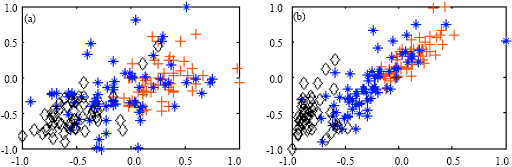
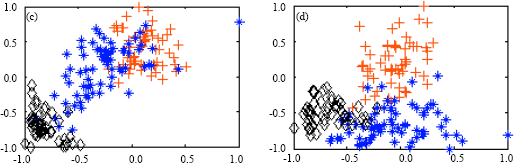
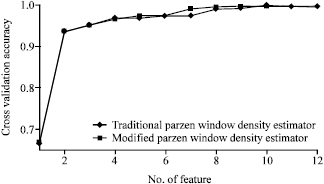
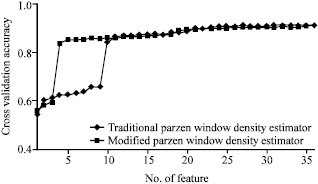
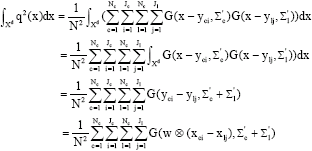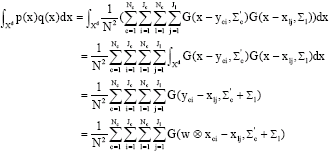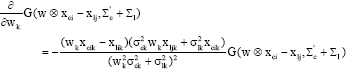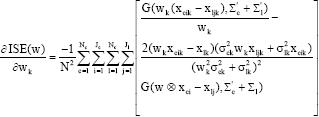Research Article
Feature Ranking by Weighting and ISE Criterion of Nonparametric Density Estimation
School of Information Engineering, Southern Yangtze University, Wuxi, China
Shitong Wang
School of Information Engineering, Southern Yangtze University, Wuxi, China