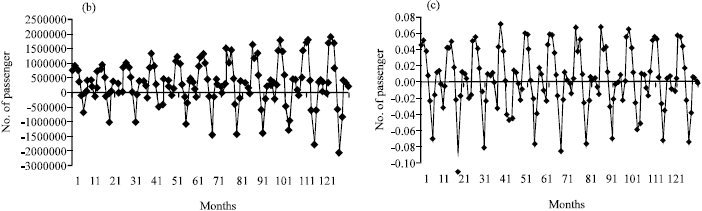
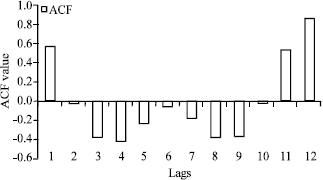
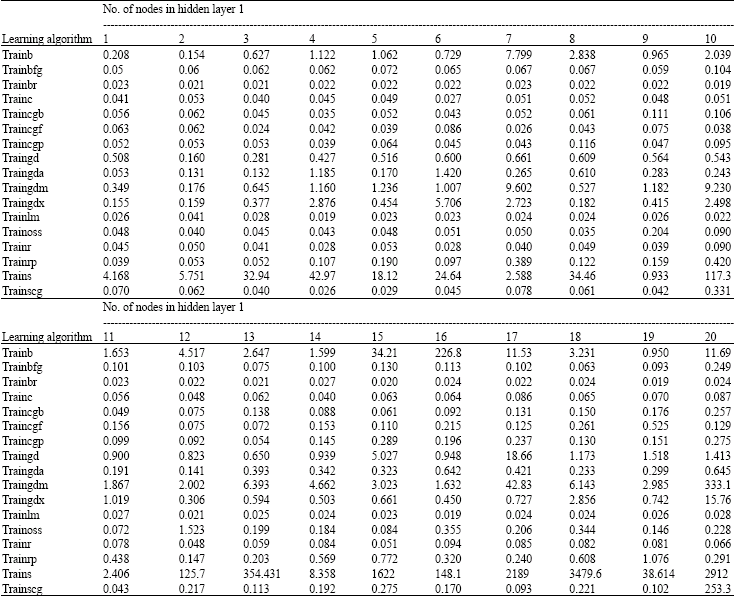
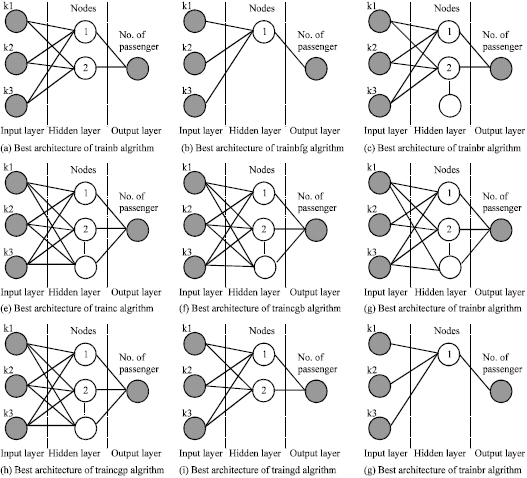
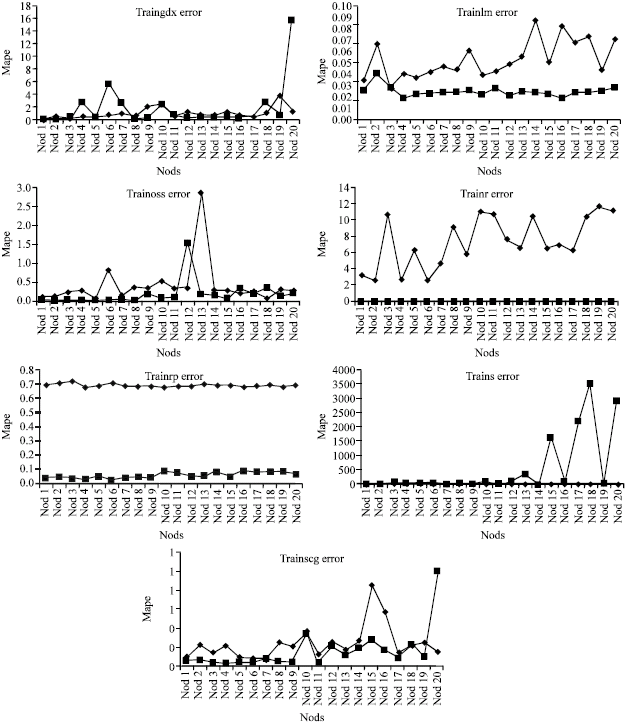
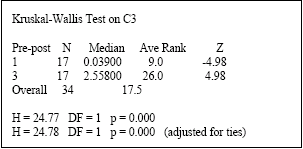
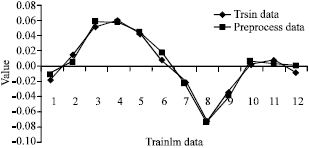
Research Article
Application of Artificial Neural Networks for Airline Number of Passenger Estimation in Time Series State
Department of Industrial Management, Faculty of Management and Accounting, Shahid Beheshti University, G.C., Tehran, Iran
A. Azadeh
Department of Industrial Engineering, Faculty of Engineering, University of Tehran, Tehran, Iran
B. Hadadi
Department of Industrial Engineering, Faculty of Mechanical and Industrial Engineering, Qazvin Azad University of Ghazvin, Iran
M. Saberi
Department of Industrial Engineering, University of Tafresh, Tafresh, Iran