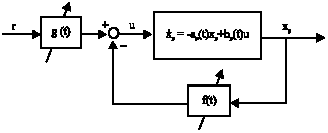
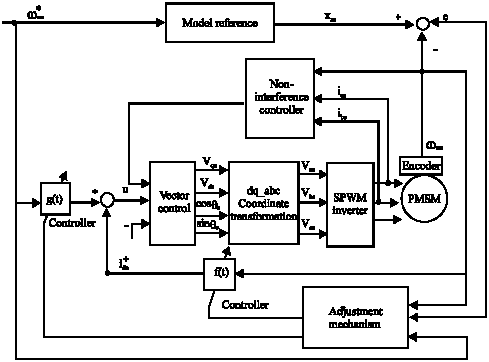
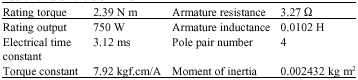
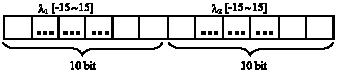
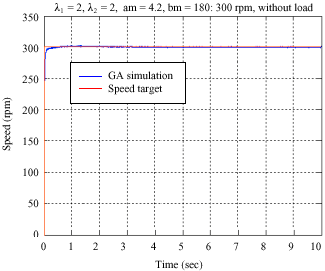
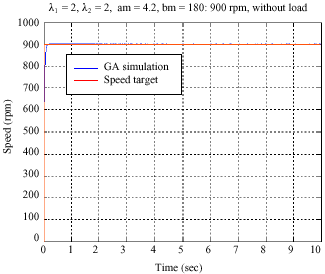
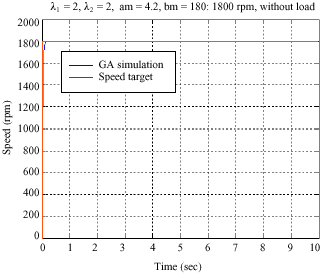
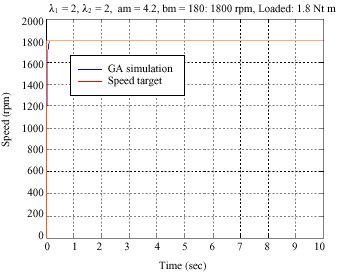
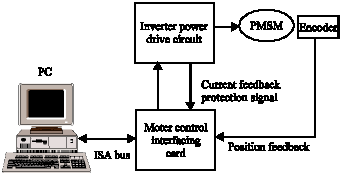
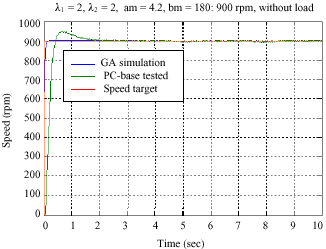
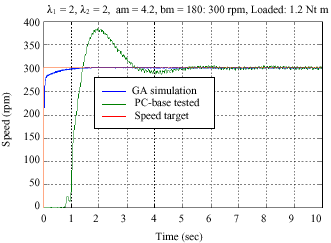
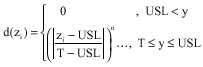Research Article
Optimization of Output Performance of Model Reference Adaptive Control for Permanent Magnetic Synchronous Motor
Department of Refrigeration and Air Conditioning, National Chin-Yi University of Technology
Shou-Ping Hsu
Department of Refrigeration and Air Conditioning, National Chin-Yi University of Technology,
Yung-Hsiang Hung
Department of Industrial Engineering and Management, National Chin-Yi University of Technology, 35, Lane 215, Section 1, Chung-Shan Road, Taiping, Taichung, 411 Taiwan, Republic of China