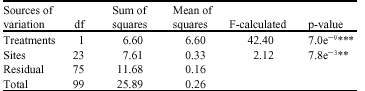
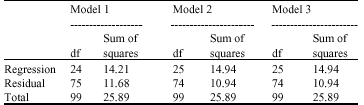
Research Article
Improving the Precision of Forestry Experimentation with Covariance Analysis
Laboratoire de Génie Forestier, Département Eaux, Forêts et Environnement,Institut National Polytechnique Houphouët-Boigny, BP 2661 Yamoussoukro, Côte d`Ivoire
J.P. Pascal
Laboratoire de Biométrie et Biologie Evolutive, UMR CNRS 5558, Université Claude Bernard Lyon 1,43 Bd du 11 Novembre 1918, 69622 Villeurbanne, Cedex France
P. Couteron
Department of Ecology, French Institute of Pondicherry, 605001 Pondicherry, India
K.B. Kouadio
Laboratoire de Génie Forestier, Département Eaux, Forêts et Environnement,Institut National Polytechnique Houphouët-Boigny, BP 2661 Yamoussoukro, Côte d`Ivoire