ABSTRACT
In this study, we give some point coincidence theorems for non-linear hybrid contractions, that is, contractive conditions involving single-valued and multi-valued mapping in non-Archimedean Menger probabilistic metric space. By using our results, we can also give common fixed theorem for single-valued and multi-valued mapping in metric space. The results presented in this research generalize and improve many results in metric spaces and probabilistic metric spaces.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.854.859
URL: https://scialert.net/abstract/?doi=jas.2008.854.859
INTRODUCTION
Let R denote the set of real numbers and R+ the non-negative real. A mapping F: R→R+ is called distribution function if its non-decreasing and left continuous with inf (F) = 0 and sup(F) = 1. We will denote D by the set of all distribution functions.
Let H denote the specific distribution function defined by:
We shall also, for convenience, adhere to the convention that for any distribution function F and for any
A probabilistic metric space (briefly, a PM-space) is an ordered pair (X, F), where, X is a set and F is a mapping of FxF into D. i.e., F associate a distribution function F(p, q) by Fp, q, where the symbol Fp, q, (x) will denote the value of Fp, q, for the argument x. the functions Fp, q, are assumed to satisfy the following conditions:
(PM-1) Fp, q = 1 for all x>0 iff p = q.
(PM-2) Fp, q (0) = 0.
(PM-3) Fp, q =Fq, p.
(PM-4) If Fp, q = 1 and Fq, r (y) = 1⇒ Fp, r (x+y) = 1.
A probabilistically normed space (briefly a PN-space) is an ordered pair (X, F) where X is a real linear space, F is a mapping of X into D. (We shall denote the distribution functions by F (x) by fx) satisfying the following conditions:
(PN-1) fx (t) = 1 for all t>0 if and only if x = 0.(PN-2) fx (0) = 0.
If we take Fx, y = fx-y, then the PN-space must be a PM-space.
A triangle inequality is said to hold in a PM-space if and only if it holds for all triple of points, distinct not, in the space.
Let Δ: [0, 1] be a 2- place function satisfying the following conditions:
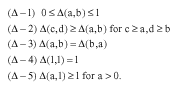 |
Menger (1942) introduced, as the generalized triangle inequality, the following condition:
(PM-5) Fp, r (x+y) ≥Δ(Fp, q (x) Fq, r (y)) for all x, y≥0, where Δ is 2-place function satisfying (Δ-1) to (Δ-5).
A Manger PM-space is a PM-space in which the condition (PM-5) holds universally for some choice of Δ satisfying the conditions:
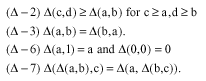 |
A triangular norm (briefly, a t-norm) is a 2-place function Δ: [0,1]x [0,1]→[0,1] satisfying the conditions (Δ-2), (Δ-3), (Δ-6) and (Δ-7).
RESULTS
We introduce the concept for compatibility for single-valued and multi-valued mapping in non-Archimedean Menger probabilistic metric spaces and give some coincidence point theorems for non-linear hybrid contractions that is, contractive conditions involving single-valued and multi-valued mapping in non-Archimedean Menger probabilistic metric space.
By using our results, we can also give some common fixed-point theorem for single-valued and multi-valued mapping in metric space.
The results presented in this study generalize and improve many results of (Kaneko and Sessa, 1989), Nadler and many others in metric spaces and probabilistic metric spaces.
Let G be the family of functions g: [0,1]→[0,∞] such that g is continuous, strictly decreasing, g (1) = 0 and g (0)<∞
Definition 1: Menger (1942); A Menger PM-space (X, F, Δ) is said to be of type (C)g if there exists a function g ε G such that:
| (1) |
for all x, y, z ε X and t≥0.
Definition 2: Nadler (1969); A non-Archimedean Menger PM-space (X, F, Δ) is said to be of type (D)g if there exists a point g ε G such that:
| (2) |
for all s, tε[0,1].
Theorem 1: Chang et al. (1994a); If a non-Archimedean Menger PM-space (X, F, Δ) is of type (D)g and then it is of type (C)g.
| (3) |
Theorem 2: Chang (1990, 1985, 1984). If (X, F, Δ) is a Menger PM-space with t-norm Δ(a, b) ≥Δm (a, b) for all a, b ε[0,1] and then it`s of type (D)g for gε G type (D)g.
Definition 3: Menger (1942). Let (X, d) be a metric space and CB (X) be the family of all non-empty closed and bounded subsets of X.
Let δ be the Hausdorff metric on CB(X) induced by the metric d, that is:
| (4) |
Theorem 3: Menger (1942); (a) (CB(X), d) is a metric space.
(b) If (X, d) is complete then (CB (X), d) is complete.
Theorem 4: Chang (1985); Let (X, d) be a complete metric space. If we define F: XxX→D as follows:
for all x, y ε X and t ε R then the space (X, F, Δ) with the t-normΔ(a, b) = min{a, b} for all x, y ε [0,1] is a τ -complet Menger PM-space.
Theorem 5: Michael (1951); If (X, F, Δ) is τ-complet PM-space with t-normΔ(a, b) = min {a, b} for all x, yε[0,1], then (X, d) is a d-complete metric space, where the metric d is defined as follows:
| (5) |
for all x, y ε X
Definition 4: Chang (1985). Let AεCB(X) and xεA. We define the probabilistic distance Fx,A between the point x and the set A as follows:
For all A, B ε CB (X) and t ε R., then ![]() is the Menger -Hausdorf metric induced by F.
is the Menger -Hausdorf metric induced by F.
Definition 5: Michael (1951); Let (X, F, Δ) be a τ-complete non-Archimedean Menger PM-space of type (D)g with the continuous τ-normΔ(a, b) = min {a, b} for all a, b ε [0,1]. Let Φ be the family of mappings φ: (R+)5→R+ such that each φ is non-decreasing for each variable, right-continuous and for any t≥0:
where the function ψ: R+ →R+ is non-decreasing, right continuous and
Lemma 1: Chang (1990). Let ψ: R+→R+ be non-decreasing, right continuous and
| (6) |
| (7) |
Definition 6: Chang (1990). Let f be a mapping from X into itself and T be a multi-valued mapping from X into Ω, where Ω is the family of all non-empty τ-closed and probabilistically bounded subsets of X. Then:
| • | The mappings f and T are said to be commuting if fTxεΩ and fTx = Tfx for all xεX. |
| • | The mappings f and T are said to be compatible if fTxεΩ and |
| For all t>0, whenever {xn} is a sequence in X such that | |
Theorem 6: Chang (1990). Any commuting mappings are compatible, but the converse is not true.
Lemma 2: Chang et al. (1994a). Let (Ω,![]() , Δ) be a Menger PM-space. Then a mapping
, Δ) be a Menger PM-space. Then a mapping ![]() from ΩxΩ into D satisfying the following conditions:
from ΩxΩ into D satisfying the following conditions:
| (1) |
| (2) |
| (3) |
| (4) |
Theorem 7: Let f be τ-continuous mapping from X into itself and ![]() be a sequence of τ-continuous multi-valued mappings from X into Ω satisfying the following conditions:
be a sequence of τ-continuous multi-valued mappings from X into Ω satisfying the following conditions:
| • | |
| • | |
| • |
For all x, yεX, t≥0 and i ≠ j, i, j = 12
where, g ε G and ψ ε Ψ.
| • | Suppose further that for any x ε X and a ε Tn x, n = 1,2, ... there exists a point b ε Tn+1 a Such that |
Proof: Since Tn(X)⊂f(X) for n = 1,2, ... by condition (4) and g ε G for an arbitrary x0 ε X, we can choose x1 ε X such that fx1 ε T1x0 ε Ω.
For this point x1 there exists a point x2 ε X such that fx2εT2x1εΩ and
| for all t≥0. Similarly, there exists a point x3εX such that |
| for all t≥0. Inductively, we can obtain a sequence {xn} in X such that |
for all t≥0.
Now, we show that the sequence {fxn} is a cauchy sequence in X. In fact by lemma 2 and conditions (3), (4), since gεG we have:
 | (8) |
If ![]() for some t0>0, from Eq. 8 and lemma (1), it follows that:
for some t0>0, from Eq. 8 and lemma (1), it follows that:
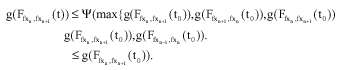 |
Which is a contradiction. Thus, for any t>0, we have
For n = 1,2, ... and so, by (8),
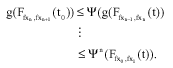 | (9) |
For all t>0. Hence, for any positive integers m,n with m>n and t>0,
 |
as n→∞, which implies that![]() for any positive integer m, that is, {fxn} is a cauchy sequence in X.
for any positive integer m, that is, {fxn} is a cauchy sequence in X.
Since (X,F,Ω) is τ-complete, the sequence {fxn} converges to a point z in X. On the other hand, by condition (7) and (9), since we have:
Letting ![]() (t)→1 as n→∞ for all t>0, that is,
(t)→1 as n→∞ for all t>0, that is,
![]() a cauchy sequence in
a cauchy sequence in![]() is τ-complete the sequence {Tnxn-1} converge to a set AεΩ.
is τ-complete the sequence {Tnxn-1} converge to a set AεΩ.
Next, we shall show that zεA. Indeed, we have:
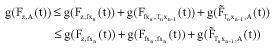 |
as n→∞ which implies Fz,A(t)→1, as n→∞ for all t>0. Thus, since AεΩ, zεA. Therefore, since f and Tn for n = 1,2, ... , we have
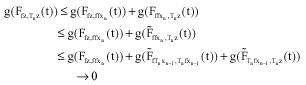 |
as n→∞ that is,![]() as n→∞. Since TnzεΩ, we have fzεTnz for n = 1,2, ... . This completes the proof.
as n→∞. Since TnzεΩ, we have fzεTnz for n = 1,2, ... . This completes the proof.
Corollary 1: Let f be τ-continuous mapping from X into itself and S, T be τ-continuous multi-valued mappings from X into Ω satisfying the following conditions:
| • | S(X)∪T(X)⊂f(X), |
| • | The pair f, S and f, T are compatible, |
| • |
for all x,y ε X and t≥0 where gεG and φεΦ. |
| • | Suppose further that for any xεX and zεX there exists a point bεTa such that: |
Proof: Taking T2n+1 = S and T2n+2 = T, n = 0,1, ..., in theorem 7, the result follows immediately.
Corollary 2: Let f be τ-continuous mapping from X into itself and ![]() be a sequence of τ-continuous multi-valued mappings from X into Ω satisfying the following conditions:
be a sequence of τ-continuous multi-valued mappings from X into Ω satisfying the following conditions:
| • | For any xεX and aεTnx, n = 1,2, ........ there exists a point bεTn+1a such that |
| • | for all x,yεX and t≥0 where gεG and φεΦ. |
Then there exists a point z ε X such that zεTnz for n = 1,2, ... , that is; the point z is a common fixed point of Tn.
Proof: Taking f = IX (the identity mapping on X) in Theorem 7, the proof follows immediately.
Definition 7: Menger (1942). A metric space (X, d) is said to be non-Archimedean if the following condition holds:
d(x, y)≤max {d(x,z), d(z,y)}, for all x,y,zεX |
Theorem 8: Chang et al. (1994b). Let f be a τ-continuous mapping from X into itself and ![]() be a sequence of τ-continuous multi-valued mappings from X into Ω satisfying the conditions:
be a sequence of τ-continuous multi-valued mappings from X into Ω satisfying the conditions:
| • | |
| • | f and Tn are compatible for n = 1,2,3, ... . |
| • | For any xεX and aεTnx, n = 1,2, ... , there exists a point bεTn+1a such that |
| • | There exists a constant k> such that : for all x,yεX and t≥0. |
Then there exists a point zεX such that fzεTnz for n = 1,2,3 ... , That is, z is a coincidence point of f and Tn.
Theorem 9: Let (X,d) be a complete non-Archimedean metric space and C(X) be the family of all non-empty compact subsets of X. Let f be a continuous mapping from X into itself and ![]() be a sequence of continuous multi-valued mappings Tn from X into C(x) satisfying the following conditions:
be a sequence of continuous multi-valued mappings Tn from X into C(x) satisfying the following conditions:
| • | Tn(X)⊂f(X) for n = 1,2, ...... |
| • | f and Tn are commuting for n = 1,2, ... . |
| • | There exists a point αε(0,1) such that For all x,yεX and I≠j,i,j = 1,2,, ... . |
Then there exists a point zεX such that fzεTnZ for n = 1,2, ... , that is, z is a coincidence point of f and Tn.
Proof: By definition (4) and condition (3), we have:
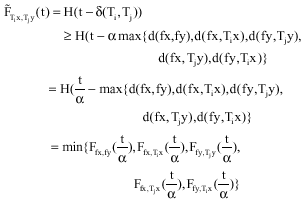 |
For all x, yεX and i ≠ j,i,j = 1,2, ... .
Moreover, for any xεX and aεTnx for n = 1,2, ... , there exists a point bεTn+1a such that:
and so we have
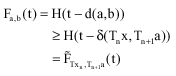 |
for all t≥0.
Therefore all conditions of Theorem 8 are satisfied and hence this theorem follows immediately. This completes the proof.
Corollary 3: Let (X,d) be a complete non-Archimedean metric space and C (X) be the family of all non-empty compact subsets of X. Let f be a continuous mapping from X into itself and T be a sequence of continuous multi-valued mappings T from X into C (x) satisfying the following conditions:
| • | T(X)⊂f(X). |
| • | f, T are commuting. |
| • | There exists an hε(0,1) such that: |
δ(Tx,Ty)≤hd (fx, fy), for all x,yεX. Then there exists a point zεX such that fzεTz.
Proof: By Definition 4 and condition 3, we have:
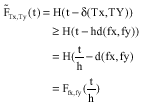 |
for all x,y ε X.
Moreover, for any xεX and aεTx, there exists a point bεTa such that:
And so we have
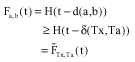 |
for all t≥0. Therefore, by theorem 8 there exists a point zεX such that fzεTz. This complete the proof.
Lemma 3: Kaneko and Sessa (1989). Let (X,d) be metric space. Let f be a mapping from X into itself and T be a multi-valued mapping from X into C(X) such that the mappings f and T are compatible. If fzεTz for some zεTz for some zεX, then fTz = Tfz.
Theorem 10: Let (X, d) and C(X) be as in Theorem 9. Let f be a continuous mapping from X into itself and T be a continuous multi-valued mapping from X into C(X) satisfying the following conditions:
| • | T(X)⊂f(X), |
| • | f and T are compatible, |
| • | There exists an αε(0,1) such that |
for all x,yεX. Suppose also that, for each xεX either (a) fx ≠ f2 x implies fx ![]() Tx or (b) fxεTx implies
Tx or (b) fxεTx implies ![]()
for some zεX. Then f and T have a common fixed point in X.
Proof: Taking Tn = T in Theorem 9 then there exists a point zεX such that fzεTz, i.e., z is a coincidence point of f and T. Then by Lemma 3, we have fTz = Tfz.
Now, by definition 4 and condition (3), we have:
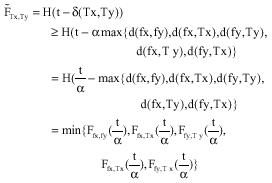 |
For all x,yεX.
Moreover, for any xεX and αεX for n = 1,2, ... , there exists a point bεTa such that:
and so we have
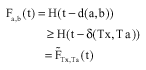 |
Since T(X)⊂f(X), for arbitrary x0εX, we can choose a point x1εX such that fx1εTx0. For this point x1, there exists a point x2εX such that fx2εTx1 and
For all t≥0 Inductively, we can obtain a sequence in X such that fxnεTxn+1 and
for all t≥0.
Then {xn} is a cauchy sequence in X. But (X,d) is complete, then xn→x.
Also the subsequences {fxn}, {Txn-1} converges to x.
Now, since f, T are continuous then fxn→fx, Tx fxn→Tx. This shows that x is a common fixed point of f, T.








