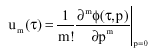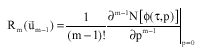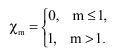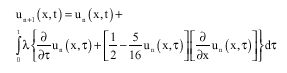Research Article
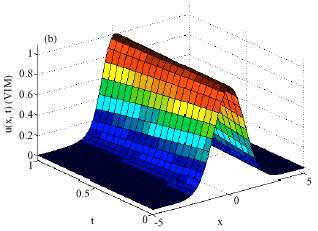
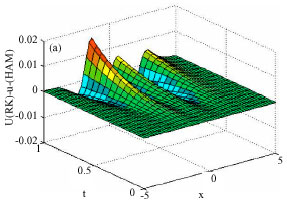
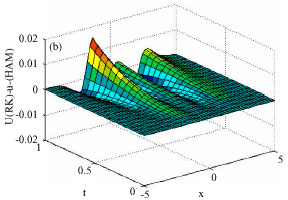
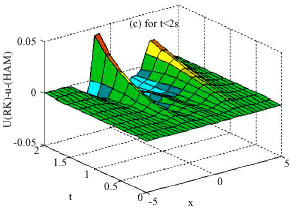
Application of Homotopy Analysis Method and Variational Iteration Method for Shock Wave Equation
Department of Mechanical Engineering, Mazandaran University, P.O. Box 484, Babol, Iran
N. Tolou
Department of Engineering, Islamic Azad University, Ayatollah Amoly Branch, P.O. Box 678, Amol, Iran
J. Mahmoudi
Department of Mechanical Engineering, K.N. Toosi University of Technology, Tehran, Iran
M. Rezvani
Department of Mechanical Engineering, K.N. Toosi University of Technology, Tehran, Iran