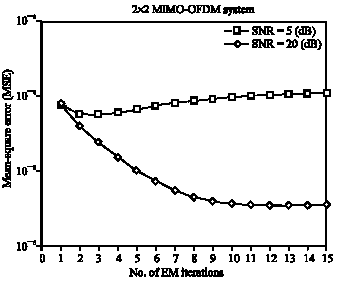
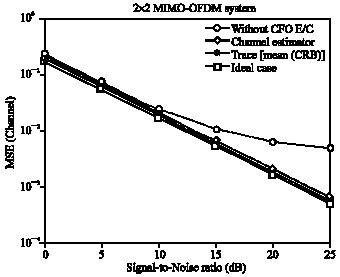
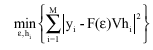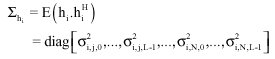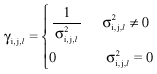Research Article
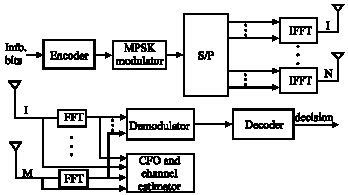
Channel and Frequency Offset Estimation for MIMO-OFDM Systems
Faculty of Electrical Engineering, K.N. Toosi University of Technology, P.O. Box 16315-1355, Tehran, Iran
M. Ardebilipour
Faculty of Electrical Engineering, K.N. Toosi University of Technology, P.O. Box 16315-1355, Tehran, Iran
M. Ahmadian
Faculty of Electrical Engineering, K.N. Toosi University of Technology, P.O. Box 16315-1355, Tehran, Iran