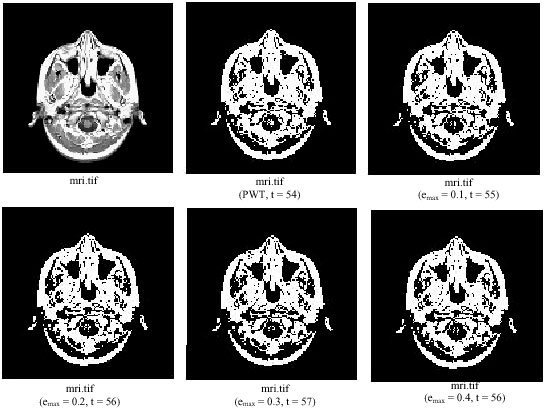
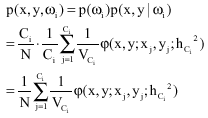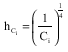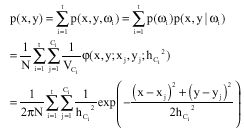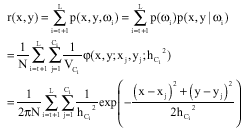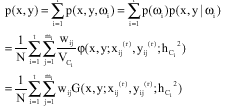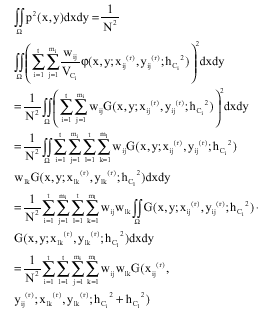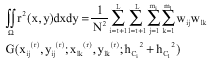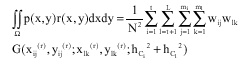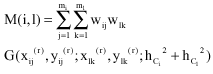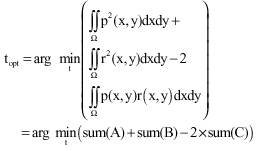Research Article
Image Thresholding Using Weighted Parzen-Window Estimation
School of Computer Science and Technology, Nanjing University of Science and Technology, Nanjing, JiangSu, China School of Information Technology, Jiangnan University, WuXi, JiangSu, China
Wang Shitong
School of Computer Science and Technology, Nanjing University of Science and Technology, Nanjing, JiangSu, China