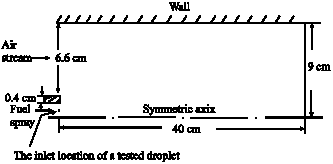
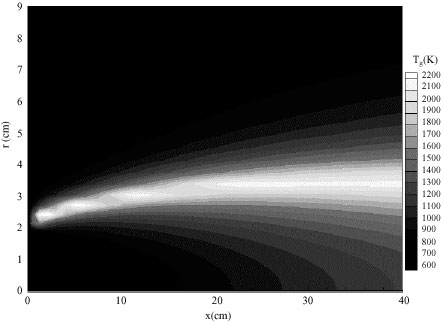
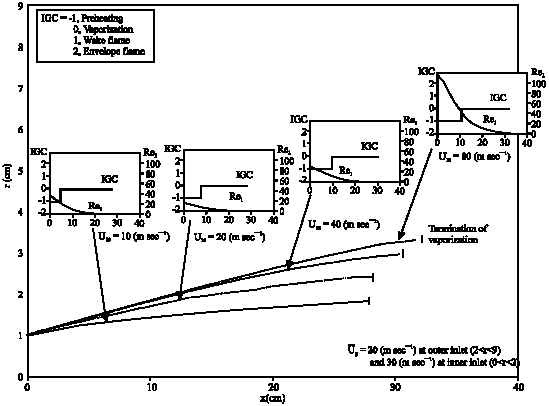
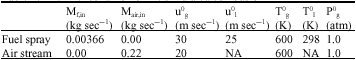Research Article
Modification of Droplet Models for Numerical Simulation in Spray Combustion Investigation
General Education Committee, Applied Technology Division, Yu-Da College of Business, Miaoli, Taiwan 36143, R.O.C
Jiunn-Shyan Huang
Department of Mechanical Engineering, Technology and Science Institute of Northern Taiwan, Taipei, Taiwan, 112, R.O.C