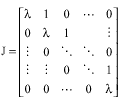
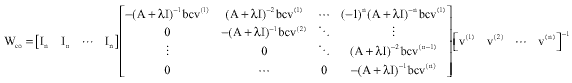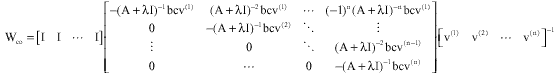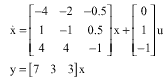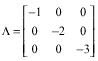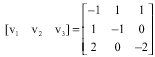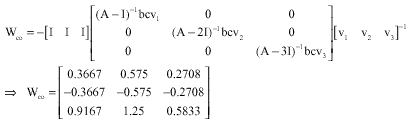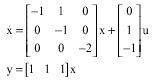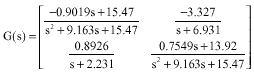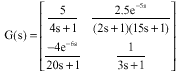Research Article
A New Approach to Compute the Cross-Gramian Matrix and its Application in Input-Output Pairing of Linear Multivariable Plants
Faculty of Electrical Engineering, K.N. Toosi University of Technology, Tehran, Iran
A. Khaki-Sedigh
Faculty of Electrical Engineering, K.N. Toosi University of Technology, Tehran, Iran