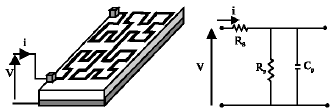
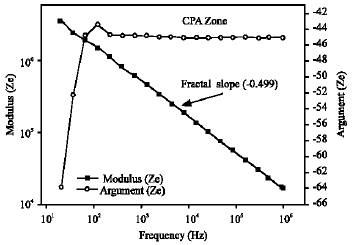
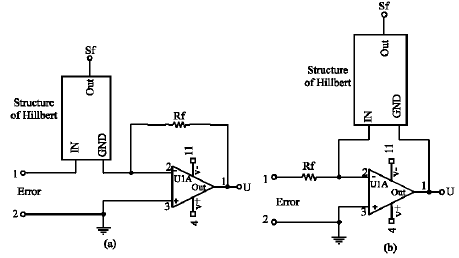
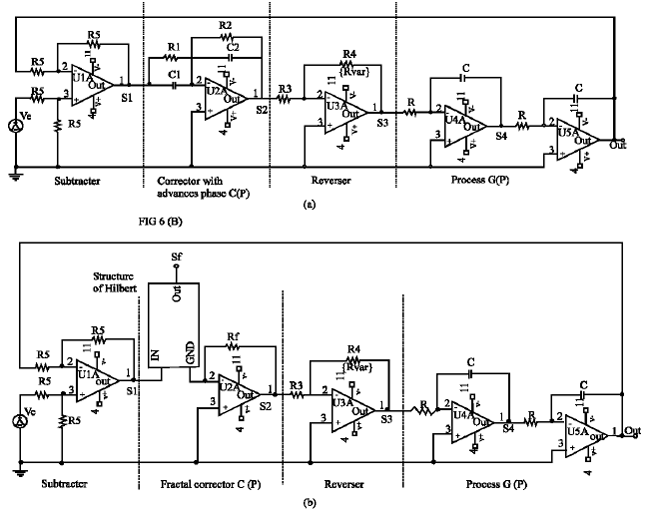
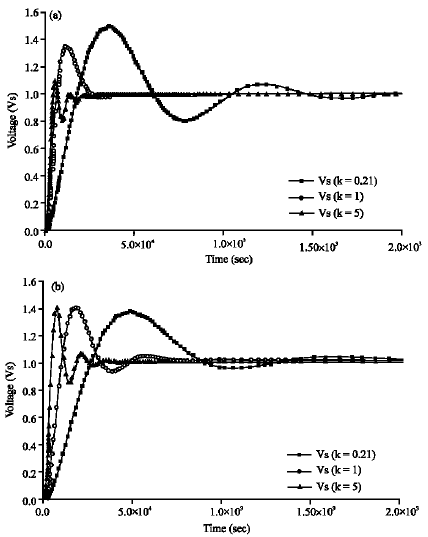
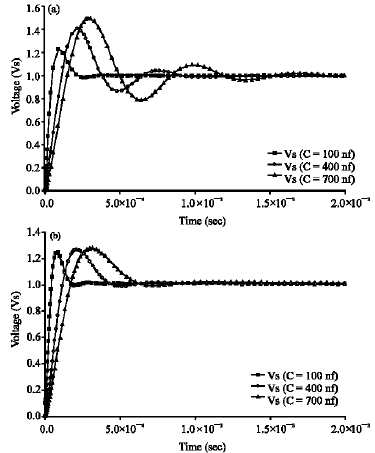
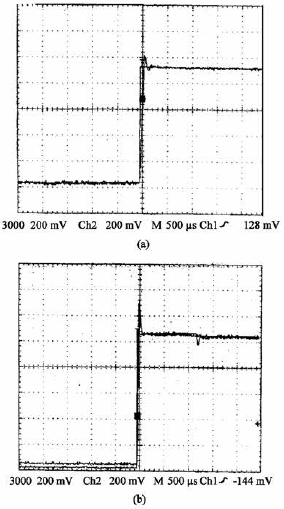
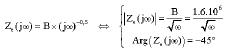Research Article
Use of a Component with Fractional Impedance in the Realization of an Analogical Regulator of Order ½
1INP-HB, Departement Genie Electrique et Electronique, BP 1093 Yamoussoukro, C�te d�Ivoire
Georges L. Loum
1INP-HB, Departement Genie Electrique et Electronique, BP 1093 Yamoussoukro, C�te d�Ivoire
Jeremie T. Zoueu
1INP-HB, Departement Genie Electrique et Electronique, BP 1093 Yamoussoukro, C�te d�Ivoire
G. Ablart
2LGET, University Paul Sabatier B�t.III R1b2, 118 Route de Narbonne, F-31062 Toulouse Cedex, France