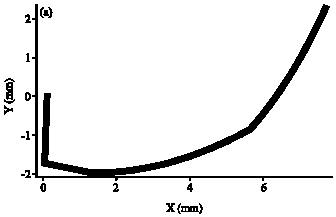
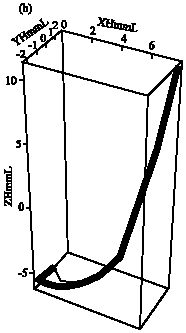
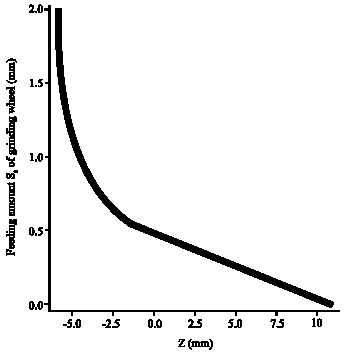
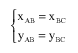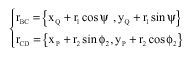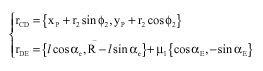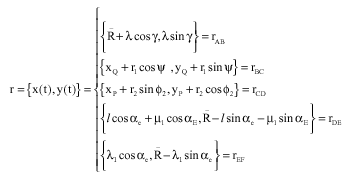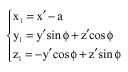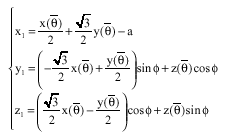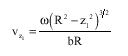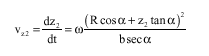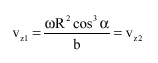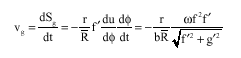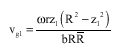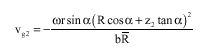Research Article
Design and NC Machining of Ball-End Taper Cutter with Constant Pitch
Department of Mechanical Engineering, De Lin Institute of Technology, Taiwan 236, Republic of China
Tian-Syung Lan
Department of Information Management, Yu Da College of Business, Miaoli County, Taiwan 361, Republic of China
Yu-Tang Chen
Department of Mechanical Engineering, De Lin Institute of Technology, Taiwan 236, Republic of China
Wei-Fang Chen
Department of Mechanical Engineering, Far East University, Hsin-Shih, Tainan County 744, Taiwan, Republic of China