Research Article
A New Approach for Isochrone Mapping in One Dimensional Flow for Using in Time Area Method
Department of Water Engineering, Faculty of Technical and Engineering, Imam Khomeini International University, Ghazvin, Iran
One of the most efficient overland flow routing methods, is Time-Area method (Ponce, 1989; Maidment, 1993; Singh, 1996). In this method, with omitting the storage effects, watershed is divided into some subareas. This is performed by constructing isochrones. An isochrone is actually a contour which passes through points of the same travel time to the outlet of the basin. Histogram of subareas, named Time-Area Histogram (TAH) is the base of the Time-Area method as a Rainfall-Runoff model.
Time to equilibrium is actually the time of wave translation. All of the area behind the wave front is in equilibrium state, which in hydraulics of surface flow means the considered area is in steady state. For a long duration rainfall, time to equilibrium at outlet is equal to time of concentration. The latter is familiar to hydrologists. Time of concentration according to definition, is the time which a drop of water needs to reach to the outlet from farthest point of watershed (Ponce, 1989; Chow et al., 1988). For constructing TAH, time to equilibrium must be divided into some equal parts, say Δt. This Δt will be used as the time difference between isochrones.
Researches on isochrone delineation methods are very limited. Henceforth almost all of the available isochrone mapping methods are empirical, approximate and without a well defined hydraulic basis. This issue introduces errors in hydrograph calculation, which are not clear in origin and magnitude.
In the present research this shortcoming of Time-Area method was investigated. Shokoohi and Saghafian (2007) had performed a research on precision of isochrone mapping methods in one dimensional (1D) flow. They showed that all of the methods define travel time (time to equilibrium for any desired point; te) as a function of travel Length (L) at a power (te ≈ Lβ). For kinematic wave, β was obtained as 5/3 and for all of the other methods the power was in a range as 0.5 to 1.5. Quoted from Shokoohi and Saghafian (2007) Time-Area method could give results as precise as analytical method if β = 1.5. In this research isochrones arranged from upstream to downstream. These conclusions have a conflict with that of kinematic wave theory.
Regarding the above literature a new research was conducted on 1D (parallel flow). The achieved results confirmed new concept of reordering isochrones and then finding a robust hydraulic based method for isochrone mapping. A noticeable outcome of the present study was the point that the best result was achieved by application a value of β which comes from kinematic wave theory.
There are two methods for studying spatial phenomena; Lumped modeling and Distributed modeling. In Lumped modeling, watershed is considered as a black box. In this box, rainfall is accepted as input and yield runoff as output at outlet. In this method which can be categorized as conceptual modeling, rainfall is related to runoff by an Input-Output model such as Unit Hydrograph model, which supposes a uniform rainfall throughout the watershed.
Lumped models without considering the spatial distribution of important properties of watersheds, take an average value for each parameter (Beven and O`Connell, 1982). In distributed modeling, in contrast to lumped modeling, modeller tries to describe and distinguish spatial pattern of all of the parameters contributing in hydrologic processes (Maidment, 1992). Almost in all of the situations, problem is solved by dividing solution domain into some squares (Raster System) or triangles TIN (Triangulated Irregular Network) System.
To achieve high precision, one needs to use distributed model which always suffers lack of one of the most important features of any efficient mathematical model; meaning simplicity (Beven, 1985). A distributed model often needs many geomorphologic related parameters such as slope, plant coverage, distribution of channel network, drainage density and infiltration capacity which are not inherently uniform (Beven, 1985). Simplicity of a model is an important property which makes it to be capable of forecasting reasonably. This property makes a model feasible and cost-effective. Simplicity of rainfall-runoff models, especially when used in real time flood forecasting framework, is an important feature of such models.
These advantage and disadvantage encourage engineers to use intermediate models. In this relation Kite et al. (1996) mentioned that when one wants to use a model to simulate a big and high extent watershed, Lumped models are not feasible and distributed models are not applicable. Quoting from Kite (1996) there are many benefits in application of intermediate models. For example such a model can obey the most important physical rules and meanwhile remains simple. Kite believed that intermediate models are capable of simulating watershed behaviour at any point and meanwhile do not need the excess amount of data which are necessary for distributed models (Kite et al., 1996).
Actually, Time-Area method is the most efficient semi-distributed model which has been developed in 1940`s. This method is known as a hydrologic watershed rainfall-runoff model. After developing and applying in Clarke conceptual model, it was used by specialists in very limited area. The main cause of this limitation was shortcoming of isochrone deriving methods. Paying attention to its power and capabilities were commenced after fast development of computer science and GIS (Geographical Information System) software. One of the most important advantages of Time-Area method is including two important geomorphologic properties of watershed; shape and drainage pattern of basin in its simulation. Time-Area method uses these two watershed properties in determining shape and peak discharge of flood hydrograph (Anonymous, 2000). It must be stated that Time-Area method success in rainfall-runoff simulation is mainly dependent on precision of isochrone mapping. According to available reports, nowadays in 40 to 60% of Corp of Engineers (USA) projects, Time-Area method is used as rainfall-runoff model (Kull and Feldman, 1998).
There are very limited researches in this domain and unfortunately almost all of the available isochrone mapping methods are experimental, approximate and do not have a well defined hydraulic base. To beginning the discussion and meanwhile illustrating importance and depth of the conducted research, a short review of theoretical basis of Time-Area and isochrone mapping methods is represented in the following section.
General equation of Time-Area method which gives a net hydrograph due to an effective rainfall is as follows:
(1) |
| j | = | Time step |
| Q | = | Discharge |
| I | = | Effective rainfall intensity |
| A | = | Area between two consecutive isochrones |
According to Eq. 1 , for applying Time-Area method, one should first delineate isochrones. Main purpose of this article is investigation on the inherent errors of the available experimental methods and meanwhile introduces a substitute hydraulic based method. In the next section these methods with a review on kinematic wave theory as analytical solution to the problem are presented. It is illustrated that in all of the methods, travel time to the basin outlet can be presented as the travel length at a power (Shokoohi and Saghafian, 2007).
Equal velocity method: Equal velocity method was introduced by Pilgrim (1977) at first. In this method Time-Area Histogram (TAH) is obtained by supposing uniformity of velocity throughout the watershed (Pilgrim, 1977). In this technique one can write:
(2) |
| tw | = | Travel time of any point to the basin outlet |
| = | Travel length |
All of the methods which Maidment (1992 and 1993), Ajward and Muzik (2000) and Melesse et al. (2003) developed for flow tracing and also the extension which works in ILWIS (GIS) (Donker, 1993), are constructed on the basis of this concept.
Laurenson method: The basic assumption of this method is the proportionality of travel time to this proportion;
in which L is travel length and S is average slope of flow path. On the other hand average slope of any route is equal to length of route divided by height difference between start and end point of the route. Then one can write:
(3) |
In this method for isochrone delineation, at first step some points are determined on elevation contours and then ordered according to ![]() 1.5. By new ordered points one can draw isochrone lines.
1.5. By new ordered points one can draw isochrone lines.
Empirical method of HEC-1: HEC-1 has a pre-assumption of Time-Area function and takes it as a parabola. This curve is used in absence of any physiographic data (Anonymous, 1991). The mentioned equation is as follows:
A = 1.414t1.5 ... (0≤ t < 0.5) | (4) |
A = 1 -1.414(l-t)1.5 ... (0.5≤ t < 1) | (5) |
In which A = Dimensionless area, meaning proportion of considered area to total area and t = Dimensionless time, meaning proportion of the considered area cumulative time to the time of concentration. If above equations are solved for ![]() in a rectangular plane (one dimensional/ parallel flow) one can write:
in a rectangular plane (one dimensional/ parallel flow) one can write:
tw ≈ | (6) |
Kinematic wave modeling: Kinematic wave equation is a simplified form of Saint Venant equations.
If all terms of momentum equation except S0 (bed slope) and Sf (energy line slope) are omitted in the Saint Venant equations, it is reduced to a uniform flow equation. A general form of resistant equation can be used as follows:
(7) |
In which Q is the discharge, Ax is the flow cross sectional area and α and β are coefficients. For Manning equation, α and β are given as follows:
(8) |
In which n and P are Manning`s roughness coefficient and wetted perimeter, respectively. By inserting resistance equation into the continuity equation, one obtains:
(9) |
| i | = | Excess rainfall intensity, |
| h | = | Flow depth, |
| q | = | Unit width discharge and |
| c | = | Kinematic wave celerity. |
Derivation of dimensionless relations for 1D flow: Consider a rectangular plane of length L and slope S0 on which a net rainfall with intensity of I and long duration falls. The latter specification about rainfall (tr ≥ te) is for guarantying the whole plane to reach to equilibrium state (Mahmood and Yevjevich, 1975). According to Eq. 9, if t0 is the time which a wave needs to translate a length x0 (from upstream) when the entire plane behind the wave front is in steady state, one can write:
(10) |
Discharge at the end of plane at time t0, will be equal to:
q0 = ix0 | (11) |
To delineate isochrones by applying kinematic wave theory, it is enough to obtain x0 in Eq. 9, for any desired number of time interval say N. Henceforth isochrones are consecutive lines which their time difference is ![]() . For example, xj corresponding to the j-th isochrone
. For example, xj corresponding to the j-th isochrone
is derived from Eq. 10 and then Eq. 11 is solved for xj = x0.
Regarding the fact that the plane totally will be translated in a time equal to te, one can write:
(12) |
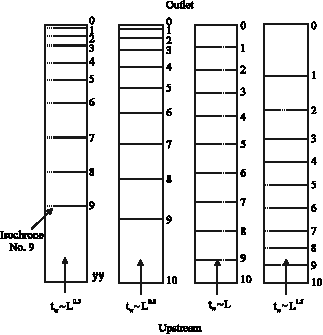 | |
| Fig. 1: | Isochrones relative position corresponding to different exponents |
Saghafian and Shokoohi (2006) obtained the following equation for calculating rising limb of a flood hydrograph, by applying Time-Area method and arranging isochrones from upstream to downstream:
(13) |
Where, q(tk) = Discharge at time tk at the end of the plane.
By using such a methodology, the Eq. 13 when arranging isochrones from downstream to upstream is changed as follows:
(14) |
As it is seen in all of the methods, tw (wave travel time) is proportional to L (travel length) at a power. To envelope all of the possible conditions, isochrones for a range of 0.5 to 1.5 were obtained and rising limb of hydrograph was calculated.
Figure 1 shows 10 consecutive isochrones for different methods (powers). It is obvious that the less the power of L, the more will be the distance between isochrones toward the upstream edge of the plane. In Time-Area method this means that the less the power of L, the less will be the contribution of watershed in supplying discharge at the start of the storm.
To determine the errors of the methods in comparison with the analytical solution, relative error was obtained by the following equation:
(15) |
In which RE is the relative error, q is the discharge corresponding to each exponent, qkw is the KW discharge and tk is the time.
To calculate a flood hydrograph due to a long duration and spatially uniform storm, with unit intensity throughout a rectangular plane with unit width, isochrones were delineated using Eq. 10 and 12 in first step. Then by applying Time-Area method for 4 conditions of different powers and also by solving the problem with kinematic wave equation independently, rising limb of the hydrograph were calculated (Fig. 2). Ordinates shows relative discharges (any discharge relative to equilibrium discharge; iL) and abscissa shows relative time (any time relative to time to equilibrium).
As it is seen from Fig. 3 the less the power of travel length, the closer were the results to analytical solution. This issue means Laurenson method is not a reliable method for isochrone mapping. Henceforth in parallel (1D) flows by choosing β = 1.67 (![]() ) hydrograph derived by Time-Area method application coincides precisely with that of kinematic wave. As it is seen, relative error of all of the methods was high at the start of storm and reduced to zero at t = te. Finally, regarding to the trend of errors it can be concluded that the closest result to analytical one belongs to the case which uses travel length at a power equal to 0.67.
) hydrograph derived by Time-Area method application coincides precisely with that of kinematic wave. As it is seen, relative error of all of the methods was high at the start of storm and reduced to zero at t = te. Finally, regarding to the trend of errors it can be concluded that the closest result to analytical one belongs to the case which uses travel length at a power equal to 0.67.
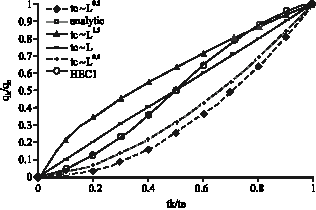 | |
| Fig. 2: | Comparison of hydrographs simulated by different isochrone mapping methods and analytical solution in 1D flow |
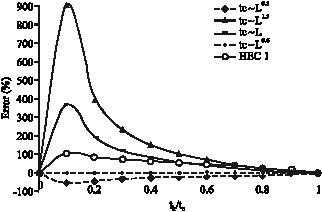 | |
| Fig. 3: | Relative errors of different isochrone mapping methods respect to analytical method in 1D flow |
This study was performed to develop a robust hydraulic based method for isochrone mapping. The past experiments for deriving isochrones obeyed arbitrary rules and the recent researches gave results in opposite side of kinematic wave model results.
It seems that outcomes of the present research could solve the most important deficiency of Time-Area method as a popular semi-distributed rainfall-runoff model.
Hydrograph derived by kinematic wave model application revealed that total discharge at outlet increases by time. This issue when using Time-Area method as rainfall- runoff model means basin contribution (the area responsible of supplying discharge at outlet) must be low in the start of storm and then increasing gradually. Regarding the basis of Time-Area method for deriving TAH, considering arrangement of sub-areas from downstream to upstream, the case where isochrones near the outlet are closer together gave the best result. According to this result, the worst or the lowest precision was obtained from the method which used ![]() 1.5 and the best or the most precise method was that one which used
1.5 and the best or the most precise method was that one which used ![]() 0.5 (Fig. 2and 3).
0.5 (Fig. 2and 3).
Time-Area method is one of the most suitable method for overland flow routing. Integrating within or linking with GIS to obtain necessary basic data gives a special place to this method. The most sensitive component of this method is isochrone mapping which divide the basin into some subbasins. Time-Area method uses TAH and multiplying it in intensity of a rainfall which is uniform in space and time to obtain flood hydrograph. Regarding the methodology of Time-Area method where diffusion and attenuation is not considered one can say that Time-Area actually is some kind of numerical solution of kinematic wave equation. The most important deficiency of Time-Area method up to now has been the use of experimental approach for isochrones mapping. The present study, succeeded in developing a methodology with a robust theoretical basis and compatible with GIS, regarding the capability of the latter to release sophisticated maps and deriving physiographical properties of basin, needed in Time-Area method.
The present research tried to find out the location of isochrones as a proportion of travel time at a power. According to the results of the present research Laurenson method as a popular one is not recommended. Another popular method, which was introduced in HEC-1, gave better result up to middle of time to peak of hydrograph. However this method showed considerable errors too.
The best method, regarding the results of the present research for calculating rising limb of hydrograph in 1D flow, was the one which uses the power derived from kinematic wave equation. However if one tends to utilize one of the available methods for isochrone delineation in 1D flows, Hec-1 approach is recommended.