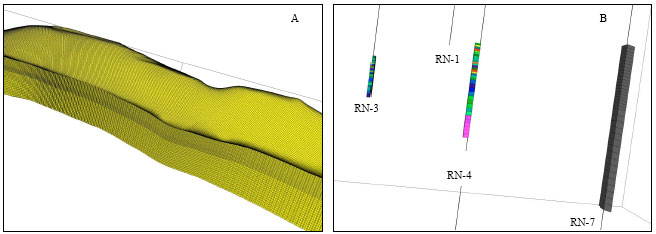
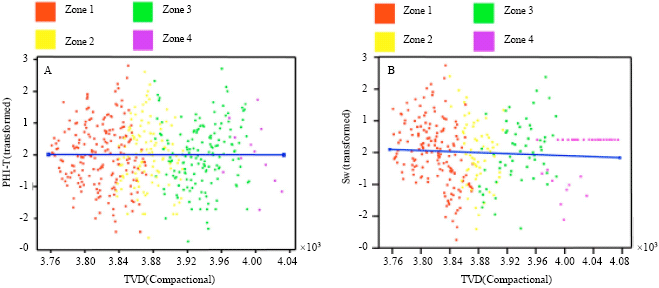
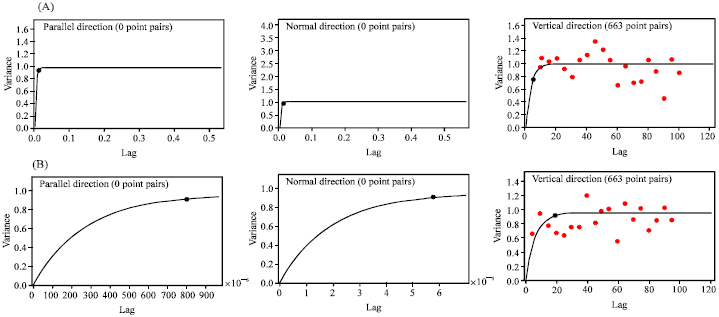
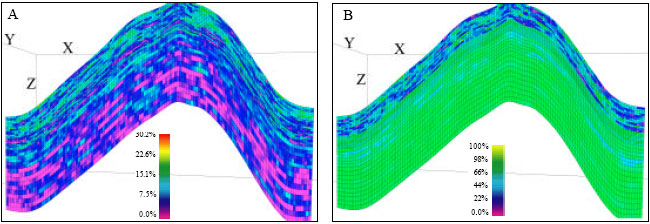
Research Article
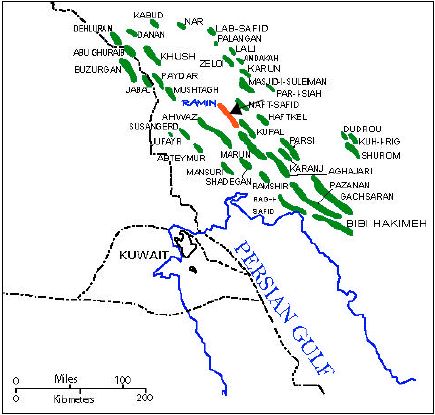
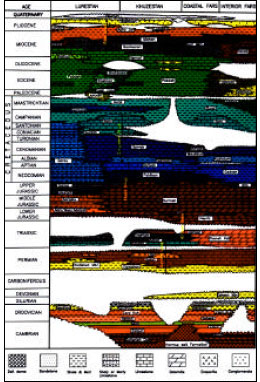
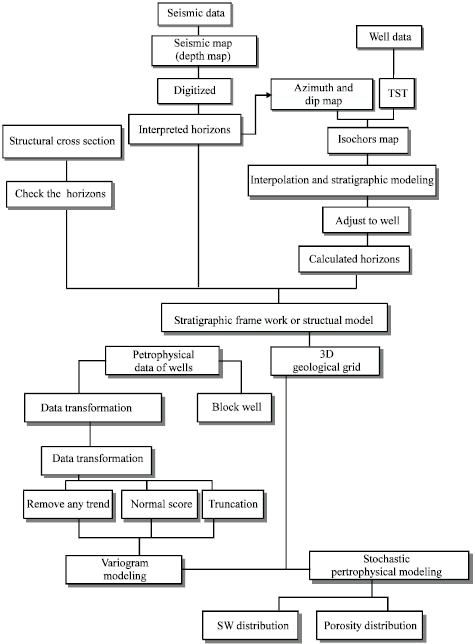
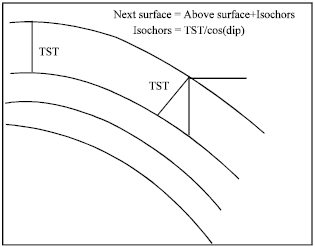
Three-Dimensional Geostatistical Modeling of Oil Reservoirs: A Case Study From the Ramin Oil Field in Iran
Department of Geology, Shahid Chamran University, Ahvaz, Iran
K. Nazari
Department of Geology, Shahid Chamran University, Ahvaz, Iran
H.A. Bakhtiar
Department of Geology, Shahid Chamran University, Ahvaz, Iran
G. Haghparast
Department of Geology, Shahid Chamran University, Ahvaz, Iran
G. Zandkarimi
Department of Geology, Shahid Chamran University, Ahvaz, Iran