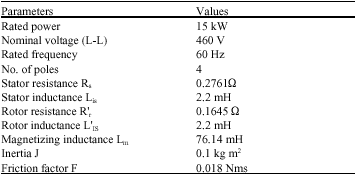
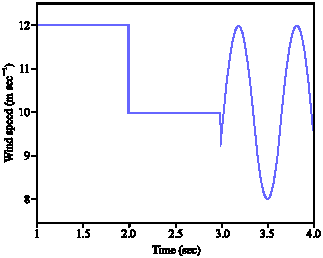
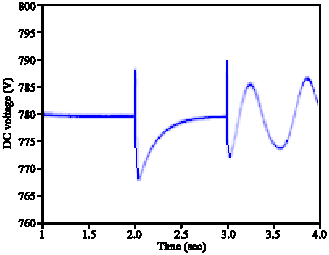
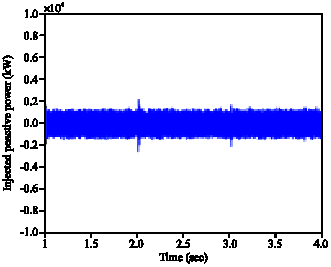
Research Article
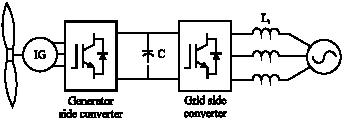
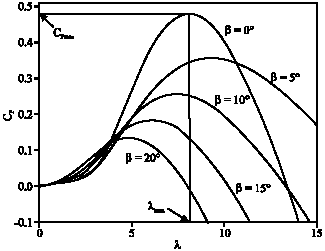
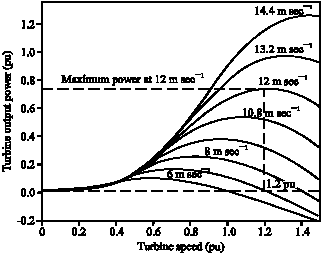
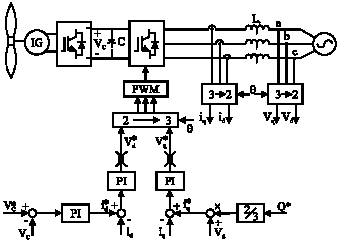
Maximum Power Control of Grid Connected Variable Speed Wind System through Back to Back Converters
Department of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran
Y. Mohamadrezapour
Department of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran
M. Hosseinpour
Faculty of Engineering, Tarbiat Modares University, Tehran, Iran
S. Torabzade
Department of Electrical and Computer Engineering, University of Tabriz, Tabriz, Iran