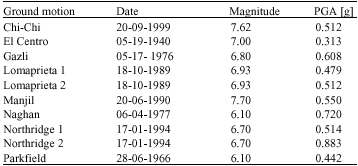
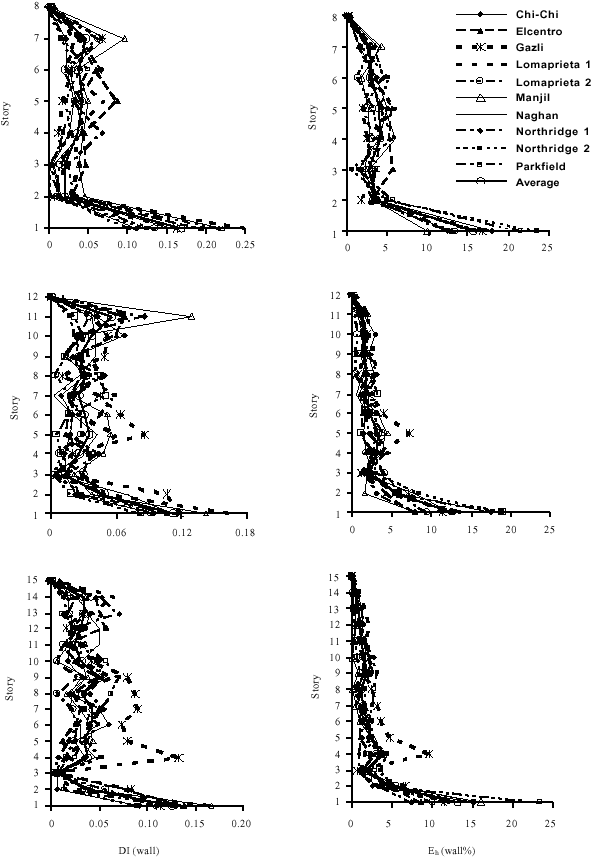
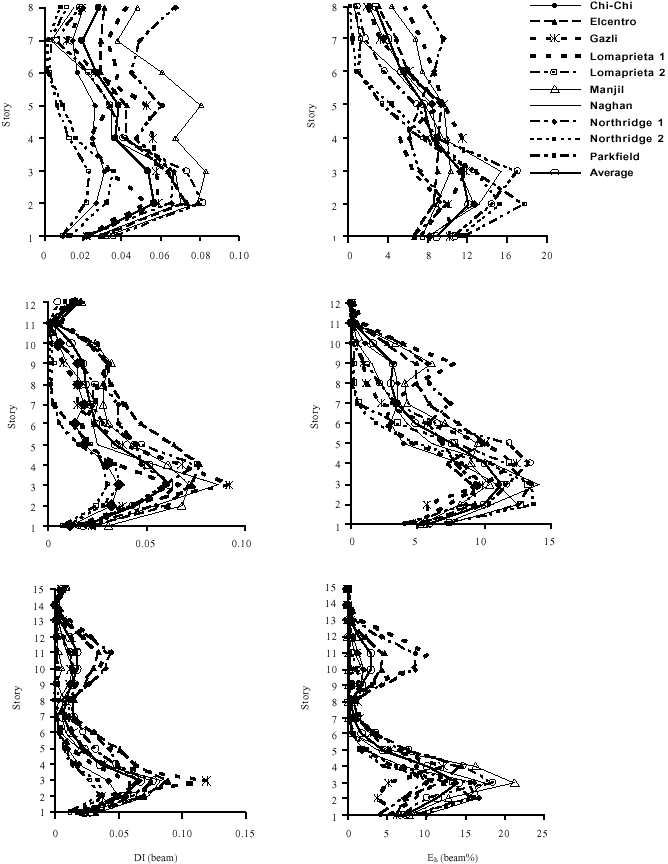
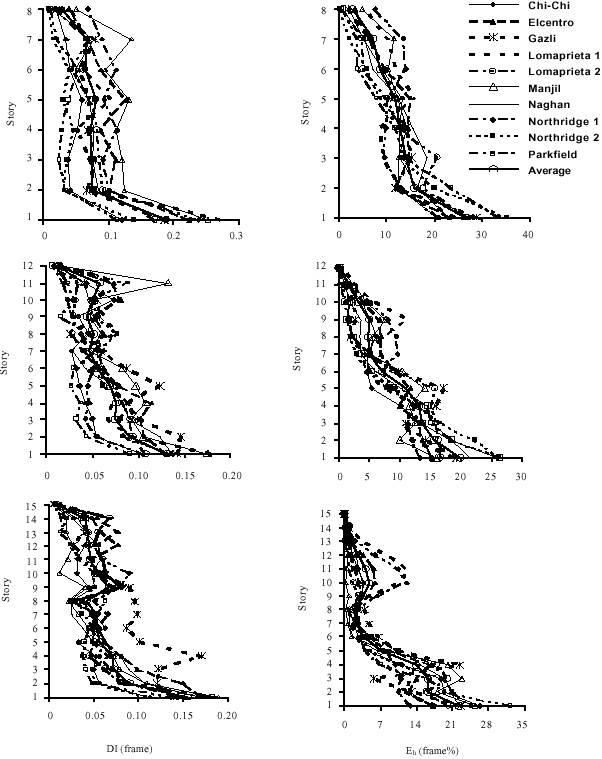
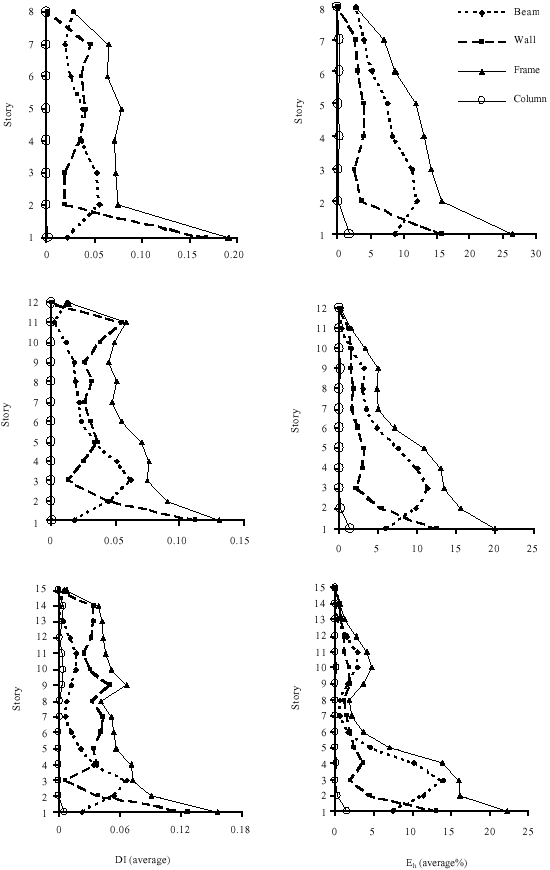
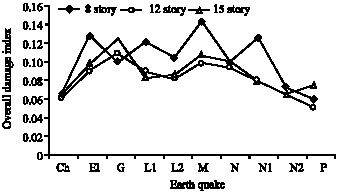
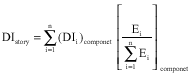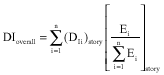Research Article
Assessment of Reinforced Concrete Buildings with Shear Wall Based on Iranian Seismic Code (Third Edition)
Department of Civil Engineering, Faculty of Engineering, Noshirvani University of Technology, Shariati Avenue, P.O. Box 47144-484, Babol, Iran
Q.Y. Ahmadi
Department of Civil Engineering, Faculty of Engineering, Noshirvani University of Technology, Shariati Avenue, P.O. Box 47144-484, Babol, Iran
B. Ganjavi
Department of Civil Engineering, Faculty of Engineering, Noshirvani University of Technology, Shariati Avenue, P.O. Box 47144-484, Babol, Iran