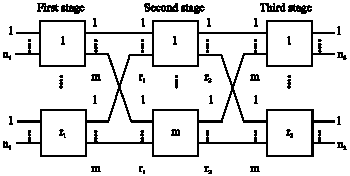
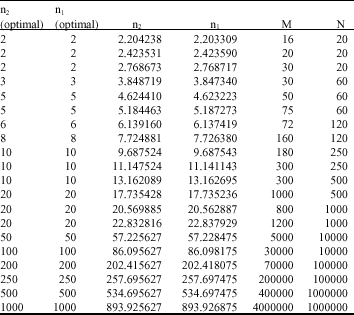
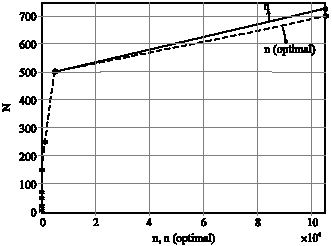
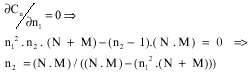Research Article
Optimal Design of Switch Sizes in Strictly Non-Blocking Clos Three-Stage Interconnection Networks
Science and Research Center, Islamic Azad University, Tehran, Iran
Mehdi N. Fesharaki
Science and Research Center, Islamic Azad University, Tehran, Iran
Mohammad Teshnehlab
Science and Research Center, Islamic Azad University, Tehran, Iran