ABSTRACT
In this study, an efficient method is proposed, which we called (TRBDO), to evaluate the probability of failure in closed-form. This method is based on the Function of random variables or transformation together with the finite element method to obtain the Probability Density Function (PDF) using the random variable transformation between the input random variables and the output variable. Once the PDF is evaluated the calculation of the probability of failure Pf is straight forward. To proof the accuracy of the proposed method, the result is compared with Monte Carlo simulation. The efficiency of presented methodology is demonstrated on the design of a 6-bar truss.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/jas.2008.4198.4203
URL: https://scialert.net/abstract/?doi=jas.2008.4198.4203
INTRODUCTION
The computational speed of computers has increased exponentially during the last 50 years. This has led to the development of large-scale simulation tools like the finite element methods, computational fluid dynamics codes, etc., for analysis of complex engineering systems. The availability of complex simulation models that provide a better representation of the actual physical system has provided engineers with an opportunity to obtain improved designs. The process of obtaining optimal designs is known as design optimization. In a deterministic design optimization, the designs are often driven to the limit of the design constraints, leaving little or no latitude for uncertainties. The resulting deterministic optimal solution is usually associated with a high chance of failure, of the artifact being designed, due to the influence of uncertainties inherently present during the modeling and manufacturing phases of the artifact and due to uncertainties in the external operating conditions of the artifact. The uncertainties include variations in certain parameters, which are either controllable (e.g., dimensions) or uncontrollable (e.g., material properties) and model uncertainties and errors associated with the simulation tools used for simulation based design (Moses et al., 2001). Uncertainties in simulation based design are inherently present and need to be accounted for in the design optimization process. Uncertainties may lead to large variations in the performance characteristics of the system and a high chance of failure of the artifact. Optimized deterministic designs determined without considering uncertainties can be unreliable and might lead to catastrophic failure of the artifact being designed. Robust design optimization and reliability based design optimization are methodologies that address these problems. Robust designs are designs at which the variation in the performance functions is minimal. Reliable designs are designs at which the chance of failure of the system is low. It is extremely desirable that the engineers design for robustness and reliability as it helps in obtaining large market shares for products under competitive economic conditions. The design of engineering structures on the basis of probability concepts will leads to more consistent safety levels, the Reliability-Based Design Optimization (RBDO) aims to find the best comprise between cost reduction and safety assurance. This approach has emerged in the last years, but the culture of deterministic design still dominates in engineering manufacture, because of significant computational effort is required to perform RBDO procedure, which it is devoted to the probabilistic constraints evaluation. The probabilistic constraints are the key in reliability-based structural design (Ang and Tang, 2006), the evaluation of these constraints create several numerical challenges associated with numerical efficiency, stability and robustness. However, several approaches has been proposed for probabilistic constraints evaluation. The probabilistic constraints are controlled by the reliability analysis, both simulations techniques and moment methods are available to carry out the reliability analysis. However, simulation techniques such as the Monte Carlo simulation is prohibitively expensive in RBDO procedure. Nevertheless, the moment methods and what is known as the first-order reliability method (FORM) (Ditlevsen and Madsen, 2005) is widely used in RBDO due to its simplicity and speed (Frangopol and Moses, 1994). Two approach are developed to ensure the reliability analysis in RBDO, it can classified into the Reliability Index Approach (RIA) and the performance measure approach (PMA) (Youn and Choi, 2004). In the RIA the probabilistic constraints are defined as the reliability indexes, evaluated by FORM. However, RIA converges slowly or even fails to converge for a number of problems. To alleviate this difficulty PMA is introduced by solving an inverse problem for the FORM, which the probability measure is converted to the performance measure. The conventional RBDO procedure is to employ nested optimization and reliability analysis loops, which the reliability analysis is estimated inside the optimization loop and herself is realized by a particular optimization procedure. This makes the computational cost of RBDO very expensive and is not suitable, especially for a complex engineering applications. In this study, an efficient method based on the transformation and the finite element method is proposed. The goal of our method is to evaluate the probability of failure in closed-form, i.e., to avoid the reliability analysis loop in the classical RBDO.
RELIABILITY ANALYSIS
The design of structures and the prediction of their good functioning lead to the verification of a certain number of rules resulting from the knowledge of physical and mechanical experience of designers and constructors. These rules traduce the necessity to limit the loading effects such as stresses and displacements. Each rule represents an elementary event and the occurrence of several events leads to a failure scenario. In addition to the vector of deterministic variables {x} to be used in the system control and optimization, the uncertainties are modeled by a vector of stochastic physical variables affecting the failure scenario. The knowledge of these variables is not, at best, more than statistical information and we admit a representation in the form of random variables. For a given design rule, the basic random variables are defined by their probability distribution associated with some expected parameters; the vector of random variables is noted herein {Y} whose realizations are written y. The safety is the state where the structure is able to fulfill all the functioning requirements: Mechanical and serviceability, for which it is designed. To evaluate the failure probability with respect to a chosen failure scenario, a performance function G(x, y) is defined by the condition of good functioning of the structure. The limit between the state of failure G(x, y)≤0 and the state of safety G(x, y)>0 is known as the limit state surface G(x, y) = 0. The failure probability is then calculated by:
(1) |
where, Pf is the failure probability, f(y)Y is the joint density function of the random variables Y and Pr[.] is the probability operator. The evaluation of integral (1) is not easy, because it represents a very small quantity and all the necessary information for the joint density function are not available. For these reasons, the First and the second order reliability methods FORM/SORM (Madsen et al., 2006) have been developed. They are based on the reliability index concept, followed by an estimation of the failure probability. The invariant reliability index β was introduced by Hasofer and Lind (1974), who proposed to work in the space of standard independent Gaussian variables instead of the space of physical variables.
RELIABILITY BASED DESIGN OPTIMIZATION
For deterministic optimization, many efficient numerical methods have been developed and applied to different kinds of structures. But for RBDO problems, the coupling between the mechanical modeling, the reliability analysis and the optimization methods represents a very complex task and leads to very high computational time. The major difficulty lies in the evaluation of system reliability, which is carried out by a particular optimization procedure (Gheng et al., 1998). Efforts were directed towards developing efficient techniques (Royset et al., 2001; Tu et al., 1999) and general proposed programs to integrate the reliability analysis for given uncertain information. These programs and procedures compute the reliability index of a structure for the defined failure modes, but do not provide an optimum set of the design parameters, in order to improve the reliability of a structure. An enormous amount of computer time is also involved in the whole design process. The sequential (or the classical) RBDO procedure and the proposed concurrent approach presented, which is based on the simultaneous solution of the reliability and optimization problems.
RBDO: Sequential approach: The sequential RBDO algorithm which is shown in Fig. 1, is calculated by nesting the two following sub-problems (Kharmanda et al., 2002):
| • | Optimization problem under deterministic and reliability constraints: |
 |
where, f(x) is the objective function, gk(x) = 0 are the associated deterministic constraints, β(x, u) is the reliability index of the structure and βt is the target reliability.
| • | Calculation of the reliability index β(x, u): |
where, d(u) is the distance in the normalized random space (Fig. 2) and H(x, u) is the limit state function in the normalized space.
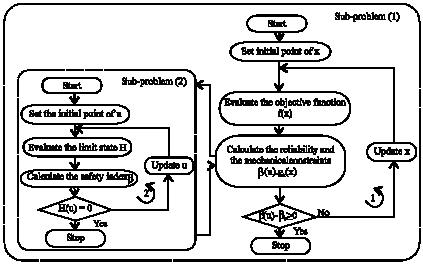 | |
| Fig. 1: | Sequential RBDO algorithm |
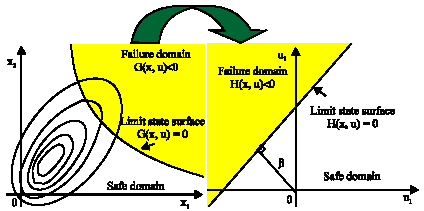 | |
| Fig. 2: | Physical space v/s normalized space |
The constrained minimization of the objective function f(x) is carried out in the physical space of design variables {x} but the reliability index β is calculated in the normalized space of random variables {u}, which are the image of {y} in the standard space. In the physical space, the image of H(x, u) is the limit state function G(x, y).
TRANSFORMATION OF RANDOM VARIABLE
The theory of the Transformation Method is based on the following theorem (Soong, 1973):
Theorem: Suppose that X is a random variable with PDF (probability density function) f(x) and A⊂![]() is the one-dimensional space where, f(x)>0. Consider the random variable (function of x) Y = u(X), where, y = u(x) defines a one-to-one transformation that maps the set A onto a set B⊂
is the one-dimensional space where, f(x)>0. Consider the random variable (function of x) Y = u(X), where, y = u(x) defines a one-to-one transformation that maps the set A onto a set B⊂![]() so that the Eq. Y = u(x) can be uniquely solved for x in terms of y, say x = w(y). Then, the PDF of Y is h(y):
so that the Eq. Y = u(x) can be uniquely solved for x in terms of y, say x = w(y). Then, the PDF of Y is h(y):
where, ![]() is the Jacobian of the transformation.
is the Jacobian of the transformation.
A new approach: Transformation-finite element method (T-FEM): The transformation method together with the finite element method is used to obtain the probability density function (PDF), in closed-form, using the random variable transformation between the input random variables and the output variable. Once the PDF is evaluated the calculation of the probability of failure Pf is straight forward.
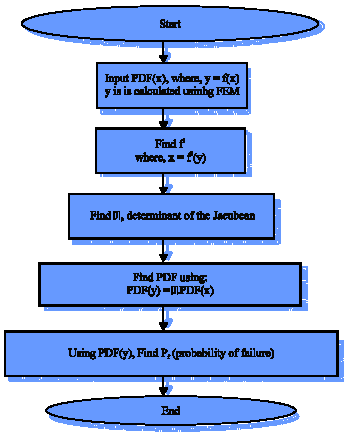 | |
| Fig. 3: | Algorithm of T-EM |
The accuracy of the solution is increased when increasing the number of elements as usual. The algorithm of this method is shown in Fig. 3.
Proposed Method: TRBDO: In this study, the inverse problem of the probabilistic transformation method has been developed. It`s shown that, if we proposed the distribution of the output variable we can calculate the exact probability density function of the input which is very helpful in the design process of a mechanical product. The accuracy of our method has been verified by 10000 simulations of Monte-Carlo.
In order to avoid the calculation of the reliability index and the separation of the solution in two spaces which leads to very large computational time, especially for large-scale structures, the transformation approach with the Finite Element Method consists in finding in one step the probability of failure i.e., the calculation of reliability index for each iteration of outer loop is not needed in other word the inner loop is not needed (Fig. 4). The optimization problem under deterministic and probability of failure constraints is:
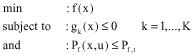 |
where, f(x) is the objective function, gk(x)≤0 are the associated deterministic constraints, Pf(x, u) is the probability of failure of the structure and Pf, t is the target probability of failure.
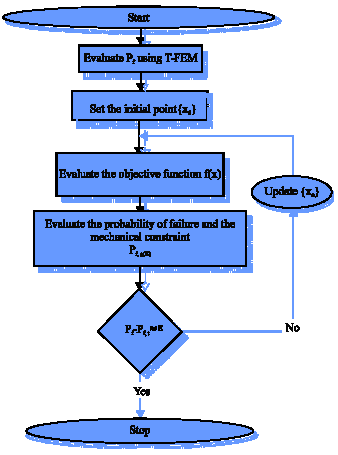 | |
| Fig. 4: | Algorithm of TRBDO |
TRBDO algorithm
Advantage of TRBDO:
| • | Using our proposed technique T-FEM, we can find the probability of failure in closed form, which is not known in general |
| • | The combination of the T-FEM and the RBDO eliminate the inner loop to find the reliability index |
| • | Work with Pf in deterministic form is more efficient and accuracy to work with the reliability index which need a numerical method to evaluate it |
Application: To illustrate the efficiency of our proposed approach (TRBDO), the 6-bar truss structure shown in Fig. 5 is analyzed:
Following, step by step the application of TRBDO:
Step 1: Modeling the Truss using FEM.
Using finite element method to obtain the displacement of node 1 and 2:
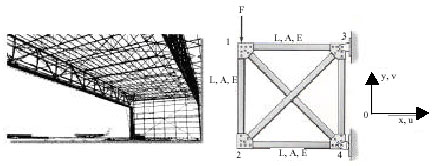 | |
| Fig. 5: | Trusses structural of aircraft hangar (left), 6-bar truss structure (right) |
Bar 3-1
Bar 4-2
Bar 4-3
Bar 2-1
Bar 3-2
 |
Bar 4-1
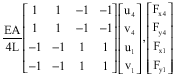 |
The assembly leads, to the global equilibrium system:
 |
Where the solution gives:
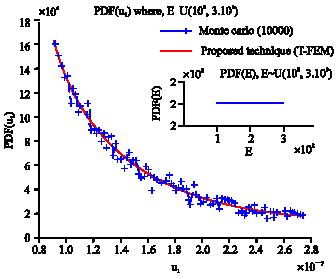 | |
| Fig. 6: | Exact PDF(u1) using T-FEM and approximate using 10000 M-C simulations |
Step 2: Using transformation technique to calculate the probability density function of the first node PDF(u1) where the Young`s modulus E is random (Fig. 6).
(a) Calculate the inverse function ![]()
(b) Calculate the Jacobean
(c) | 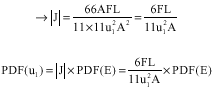 |
let us suppose E~U(108, 3.108)
Step 3: Let us consider the displacement of node 1 is considered as limit-state function. Find the probability of failure Pf where, for example, u1,limit = 2.10-7
Step 4: TRBDO formulation: It is request to minimize the cross section (A)of the bar, where F = 10 N and L = 10 mm.
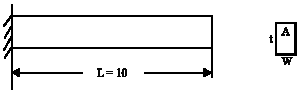 |
The TRBDO approach is now formulated as:
 |
The solution of the above problem is w = 2.4781, t = 3.8421. The comparison with classical RBDO shows that the computation time is divided by more than 100, when the PTM is applied.
CONCLUSION
The coupling of optimization and reliability problems allows us to obtain the best compromise between cost and safety. But this coupling represents a very complex task and leads to very high computational time. The major difficulty lies in the evaluation of system reliability which is carried out by a particular optimization procedure. The proposed method, which we call it TRBDO, avoid this coupling and avoid the searching of reliability index. The proposed method gives us the probability of failure in closed form in one step. The efficiency of the new method is confirmed by several applications on structures; a 6-bar truss problem is shown in this study.
REFERENCES
- Ditlevsen, O. and H. Madsen, 2005. Structural Reliability Methods. 1st Edn., John Wiley and Sons, New York, ISBN: 0-471-96086-1.
Direct Link - Moses, F., E. Aktas and M. Ghosn, 2001. Cost and safety optimization of structural design specifications. Reliability Eng. Syst. Safety, 79: 205-212.
CrossRef - Youn, B.D. and K.K. Choi, 2004. Selecting probabilistic approaches for reliability-based design optimization. AIAA. J., 42: 124-131.
Direct Link - Hasofer, A.M. and N.C. Lind, 1974. An exact and invariant second moment code format. J. Eng. Mech. Division, 100: 111-121.
Direct Link - Gheng, G., G. Li and Y. Cai, 1998. Reliability-based structural optimization under hazard loads. Struct. Optim., 16: 128-135.
CrossRefDirect Link - Royset, J.O., A. Der Kiureghian and E. Polak, 2001. Reliability-based optimal structural design by a decoupled approach. Reliability Eng. Syst. Safety, 73: 213-221.
CrossRef - Tu, J., K.K. Choi and Y.H. Park, 1999. A new study on reliability-based design optimization. J. Mech. Des., 121: 557-564.
CrossRef - Kharmanda, G., A. Mohamed and M. Lemaire, 2002. CAROD: Computer-aided reliable and optimal design as a concurrent system for real structures. Int. J. CAD/CAM., 2: 1-22.
Direct Link








