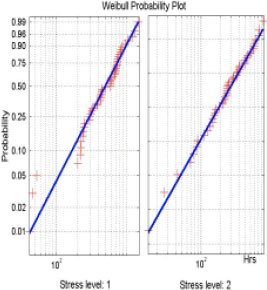
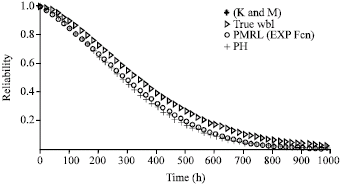
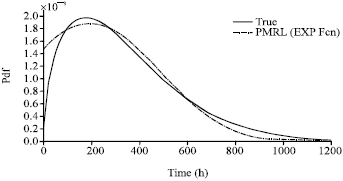
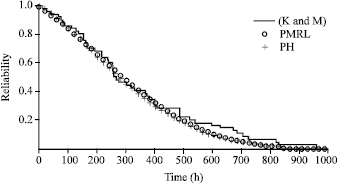
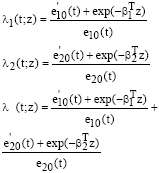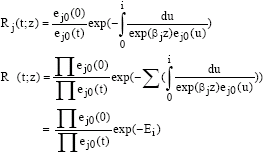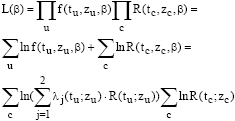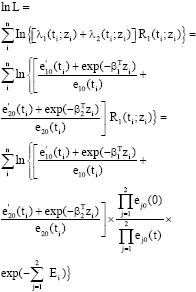Research Article
Accelerated Life Testing Based on Proportional Mean Residual Life Model for Multiple Failure Modes
Faculty of Engineering, Ferdowsi University of Mashhad, Mashhad, Iran
N. Dehqanmongabadi
Faculty of Engineering, Ferdowsi University of Mashhad, Mashhad, Iran