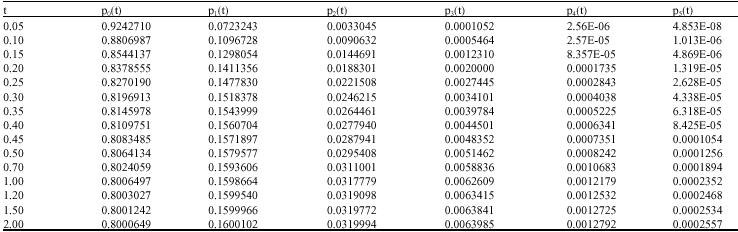
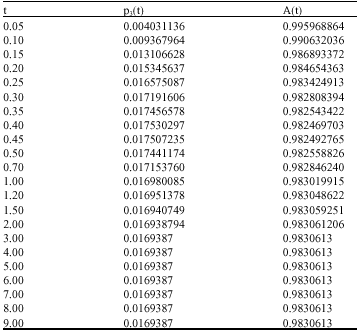
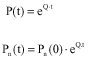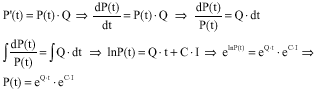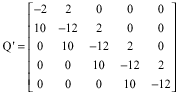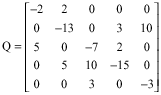Research Article
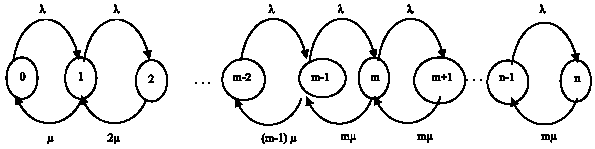
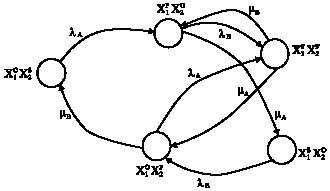
A Methodology for Analyzing the Transient Availability and Survivability of a System with the Standby Components in Two Cases: The Identical Components and the Non-Identical Components
Department of Industrial Management, Allame Tabatabaee University, Tavanir Avenue, Tehran, Iran
F. Ghassemi-Tari
Department of Industrial Engineering, Sharif University of Technology, Tehran, Iran
A. Mohtashami
Department of Industrial Management, Allame Tabatabaee University, Tavanir Avenue, Tehran, Iran
J.S. Sadaghiani
Department of Industrial Management, Allame Tabatabaee University, Tavanir Avenue, Tehran, Iran