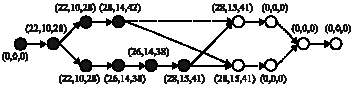
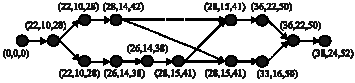
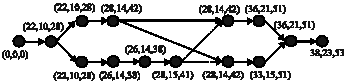
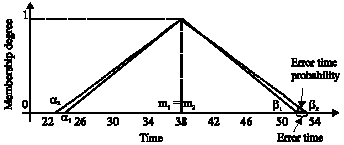
Research Article
Continuous Fuzzy Longest Path Problem in Project Networks
School of Railway Engineering, Iran University of Science and Technology, 16846-13114, Tehran, Iran
A.R.J. Moghadam
School of Railway Engineering, Iran University of Science and Technology, 16846-13114, Tehran, Iran