Research Article
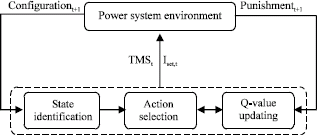
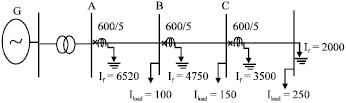
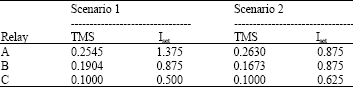
Q-Learning Based Cooperative Multi-Agent System Applied to Coordination of Overcurrent Relays
Department of Electrical Engineering, Faculty of Engineering, Ferdowsi University of Mashhad, Mashhad, Iran
M. Rahimiyan
Department of Electrical Engineering, Faculty of Engineering, Ferdowsi University of Mashhad, Mashhad, Iran