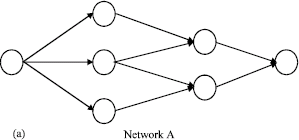
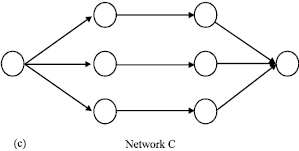
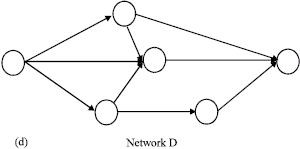
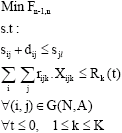Research Article
Development of a Constructive Heuristics Rule for Constrained Resource Allocation in Stochastic Networks
Department of Industrial Engineering, University of Tehran, P.O. Box 11365, 4563 Tehran, Iran
S. Baradaran
Department of Industrial Engineering, Amirkabir University of Technology, 424 Hafez Avenue, Tehran, Iran
S.M.T. Fatemi Ghomi
Department of Industrial Engineering, Amirkabir University of Technology, 424 Hafez Avenue, Tehran, Iran
S.S. Hashemin
Department of Industrial Engineering, Islamic Azad University, Ardabil Branch, Ardabil, Iran