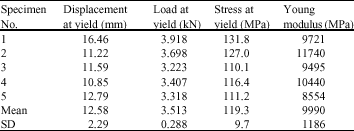
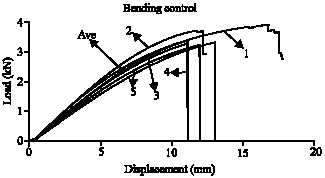
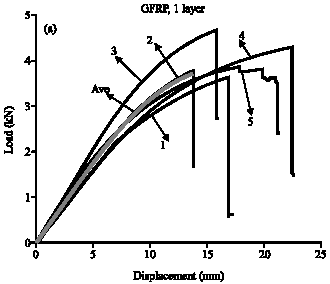
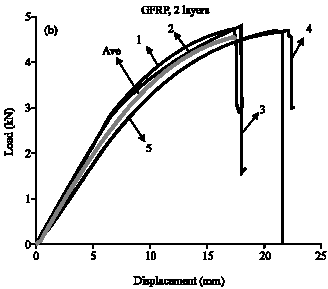
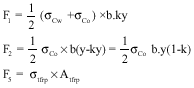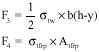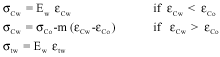Research Article
Experimental and Analytical Investigations on Flexural Strengthening of Old Wood Members in Historical Buildings with GFRP
Faculty of Civil Engineering, Technical University of Babol, Tehran, Iran
Y. Gholipour
School of Civil Engineering, University of Tehran, Iran
Gh. Ebrahimi
Faculty of Natural Resources, University of Tehran, Iran
M. Hosseinalibeygi
Department of Civil Engineering, University of Mazandaran, Iran