INTRODUCTION
Encryption is used to provide privacy of data, that is, to keep the data
secret from people other than the intended recipients (Jutla, 2001). It
has a significant advantage, which is the encryption operations don`t
depend on each other there`s no chaining (Rogaway and Shrimpton, 2006).
Message authentication, also often called message integrity, provides
assurance to the recipient of the data that it came from the expected
sender and has not been altered in transit (Black and Rogaway, 2005).
The reality is that you need both mechanisms, even to get just privacy.
Using both encryption and message integrity and they`re both somehow based
on cryptographic primitives, obviously you should be able to make savings
by somehow combining common operations. It turns out that you can, but
it`s a much more subtle process than you might at first think messages
(Dworkin, 2005; Rogaway and Shrimpton, 2006; Boneh et al., 2004;
National Institute of Standards and Technology, 2001; Lee, 1999).
Encryption alone isn`t sufficient to ensure privacy. Several researches
provide a number of failure modes in IPsec when encryption alone is applied
(Ferguson, 2002). The 802.11 WEP (Wired Equivalent Privacy) demonstrates
this failure in a very simple manner (Cam-Winget et al., 2003;
IEEE, 1999). Researchers had a short discussion with links about other
reasons for always using a message authentication code, not only when
message integrity is required, but also when data confidentiality is needed
were instigated (Rogaway and Shrimpton, 2006; Bellare et al., 1996;
National Institute of Standards and Technology, 1985).
Message authentication code: To guarantee message integrity, you
can either use public-key digital signatures (which are computationally
very expensive and have other problems) or you can use a MAC (Message
Authentication Code). A MAC can be thought of as a keyed hash. There are
a number of different ways to create MACs such as HMAC, CMC-MAC and Carter-Wegman
MAC (Black and Rogaway, 2005; Dworkin, 2005; Cary and Venkatesan, 2003;
IEEE, 1999).
In combined modes using block ciphers, two lots of processing are used
on the data, one to encrypt it and one compute a MAC. While thinking about
all of this, two new requirements arose:
| • |
It should be possible to MAC a whole packet, while only
encrypting part of it. |
| • |
It should be possible to parallelize the underlying operations,
to enable high throughput if you`re prepared to throw extra hardware
at the problem. |
The current IPsec solutions, based on CBC mode encryption and HMAC, take
care of the first of these, but not the second; both operations are inherently
sequential in nature because of the chaining (Black and Rogaway, 2005).
After the multiple security problems with 802.11 WEP, there was pressure
on the IEEE standards committee to do something secure for a change (Ferguson,
2002; IEEE, 1999). This committee didn`t have the kind of cryptographic
expertise needed to design the solution from the ground up, as they had
already demonstrated, so, they wanted to adopt a single, easy-to-use package
solution. OCB mode was proposed but patent considerations apparently prevented
its adoption (Rogaway et al., 2001).
CCM: CCM (Counter with CBC-MAC) mode was eventually specified
by a group of consultants and adopted for the next generation of 802.11
wireless security. (There`s also an intermediate patch that many manufacturers
have adopted, but I`m referring here to the real solution.) CCM is, cryptographically
speaking, quite straightforward (Rogaway and Wagner, 2003). The supplied
key is used to derive separate keys for encryption and integrity protection,
then the encryption is done using counter mode, while the MAC is calculated
using CBC-MAC, both as mentioned above. A header is prep ended to the
data, including the length of the message and associated unencrypted data.
Because this mode was specifically designed for 802.11, it meets those
requirements very well, but has been criticized for general purpose use
on the grounds that the header means you can`t process a stream of data
(you need to know the length of it before you can begin processing), it
can`t be parallelized (because of the use of CBC-MAC) and the format of
the header is a bit fiddly (to keep it very small based on 802.11 requirements)
(Dworkin, 2005).
EAX: EAX (Encrypt then Authenticate then Translate) mode is very
similar in concept to CCM mode and was developed to address the criticisms
mentioned earlier. These authors coined a new term, AEAD (Authenticated
Encryption with Associated Data) for the problem of encrypting partial
packets while authenticating all of them (Bellare et al., 2004).
In essence, this method still boils down to using Counter Mode to encrypt
the data and CBC-MAC to create the MAC. The last block of input for the
MAC is processed in a special manner to prevent attacks that work by appending
data, but without introducing a dependency on the length of the data or
extending it with unnecessary padding. Again, because of the use of CBC-MAC,
it still cannot be completely parallelized (Black and Rogaway, 2005; Ferguson
et al., 2003; Bellare et al., 1996).
THE PROPOSED TECHNIQUE (ZBM)
The key: THE ZBM fundamentally uses a 256 bits key which will
be used also to extract 2 Numbers K1 and K2. K1‘s
value ranges between 1 and 256 and K2‘s value ranges
between 1 and 16.
However, you may just set the 2 values manually, this will also produce
K1 and K2.
The ZBM description: The technique that will be used to produce
the ZBM based on DES key is as follow:
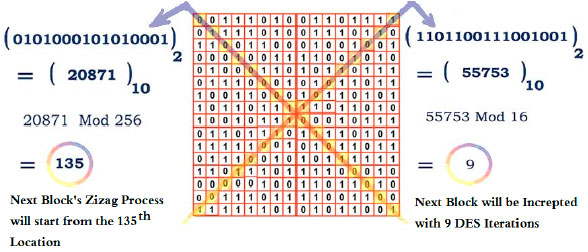
First, if K1 and K2 are not detected calculate
them as shown in Fig. 1.
Second, the first block will be zigzagged in the file based on K1
value, so that K1-1 cells will be skipped in the zigzag then
starts zigzagging from the K1`th Cell up to the end of the
block then go back to the skipped K1-1 values as shown in Fig.
2 where K1 = 25 and K2 = 6, this will distribute
the original key bytes in fair way and will be useful in the next step
which is to produce the 2k numbers K1 and K2.
Figure 3 shows how good the zigzag operation as a technique
of distribution is. The image shows the Permutation in case of starting
from the first position but when starting from another position it will
be totally different one.
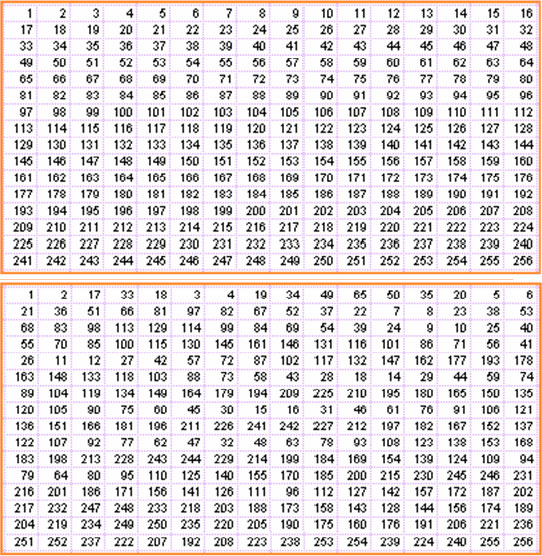
Third, regenerate the 2 k numbers K1 and K2 by
apply the first step on the generated block. These keys will be used for
the next block as shown in Fig. 4.
Fourth, the generation of the 263 bit ZBM key is based on the DES key.
 |
| Fig. 1: |
Calculating K1 and K2 values |
 |
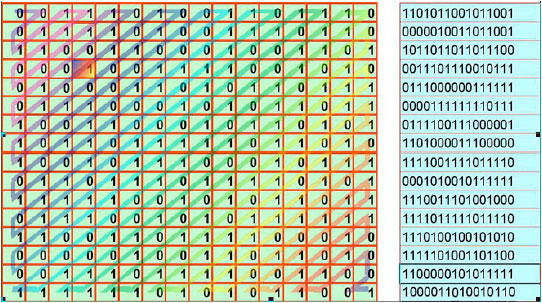| Fig. 2: |
Starting the zigzag process from location K1 (25) of
the zigzag |
 |
| Fig. 3: |
How zigzag distributes bits incase it starts from the
first location |
 |
| Fig. 4: |
Calculating K1 and K2 values which
will be used for the next block |
 |
| Fig. 5: |
Counting the number of one-bits in the diagonal order |
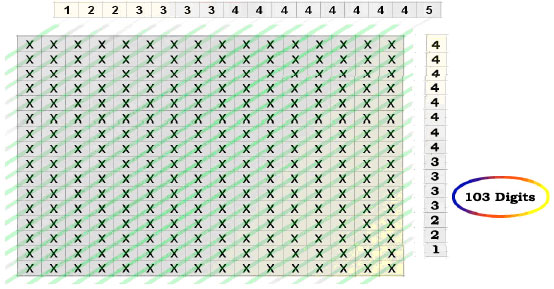
This process stands on counting the number of one-bits in the diagonals, in the rows and finally in the
columns as shown in Fig. 5-7, respectively. Note that
the same process will be used to produce the ZBM block in every iteration.
These values will be saved as binary by dedicating proper sizes of bits
for all entries. The number of bits dedicated for each entry was chosen
based on the max value for that entry. Figure 8 shows
how every cell is represented within three entries and Fig.
9 shows how the 263 bits key is collected.
Fifth, using the above 263 bits key and the 2 numbers K1 = 25 and
K2 = 6, K1 will force zigzagging process of the First
ZBM block to start from location 25 and K2 will guide the algorithm
to take the next block data from the 6th DES iteration. However, these two values
will be changed for the next block and for every block after it as shown in
the third step, this will give the algorithm its strength, so that if 1 bit
was modified in any block, then this will give a fully different ZBM block values.
Sixth, once the 263 bits block is produced, the chaining process is started
using addition and mod operations on parts of 25 bits of the block as
shown in Fig. 10.
Chaining in the ZBM is not like the normal CBC MAC chaining, as new factors
effect on the blocks chaining process, Fig. 11 shows
how can this be achieved.
Advantages of the ZBM: The ZBM inherits DES strength points, this
include all the security features of block cipher in general, it also
add to this the strength of its longer key of 263 bits and the two K-values
which will absolutely make it much more difficult to inference the original message
based on the final ZBM.
 |
| Fig. 6: |
Counting the number of one-bits in the row order |
 |
| Fig. 7: |
Counting the number of one-bits in the column order |
 |
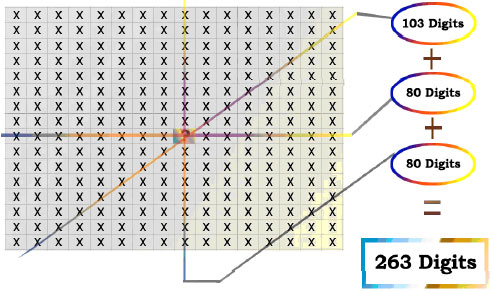| Fig. 8: |
How every cell is represented within three entries |
 |
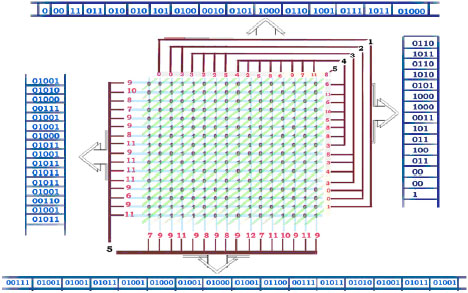| Fig. 9: |
How the 263 bits key is collected |
|
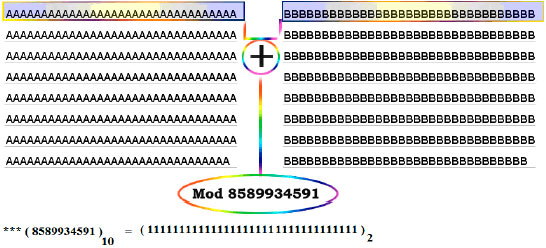| Fig. 10: |
The chaining process using addition and mod operations
on parts of 25 bits of the block |
|
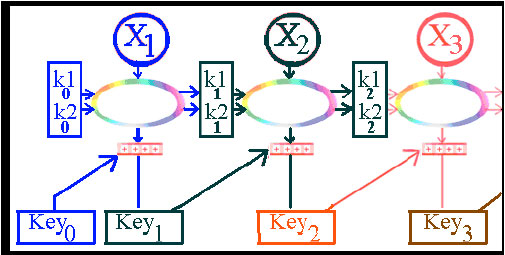| Fig. 11: |
Calculating K1 and K2 values which will be used for
the next block |
By choosing just one DES iteration for each block in the message with
a strong function which is difficult to revert, more strength will be
added and also MACing time will be reduced. Note that being based on DES
algorithm here does not mean that the encryption has to be applied when
the message is MACed, just one iteration of DES is used for each block
of the message in a semi random but strict technique. This technique can
surmount most of the CBC MAC chaining drawbacks; this is done by using
different values of K1 and K2, which make dropping
or changing one bit from the message a reason for changing the whole ZBM
value.
Drawbacks of the ZBM: Still the values of K1 and K2
between 0 and 256 is a very small number and make the ZBM subject to brute
forcing the block size on which the ZBM and DES which ZBM is based on-is
a small one However, this do not mean that the technique as a whole is
a weak one. Comparing to the well known MACing and hash function the 256
bits block size is a small size, but this can be counted as an advantage
of the technique.
CONCLUSION AND FUTURE WORK
Cryptography is hard to get right and it has recently become clear that
combining encryption and authentication to get practical security is downright
difficult. This study introduced a new method that can be ensuring a minimum
of Authenticity and work effectively. ZBM initiated some modifications
on the Chaining MAC with DES algorithm; this gave a light on how stronger
cipher algorithms like AES, RSA and blowfish can be exploited with some
strict process toward stronger MAC algorithms.
Subscribe Today
