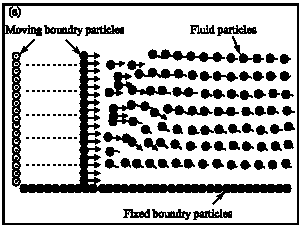
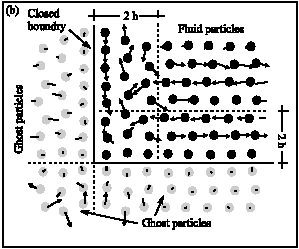
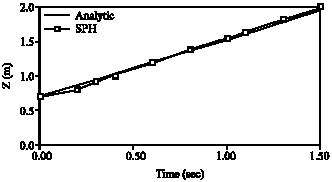
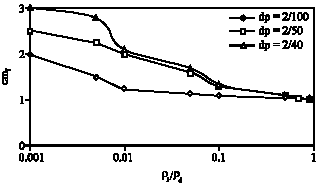
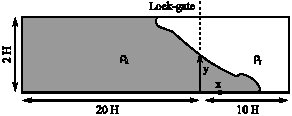
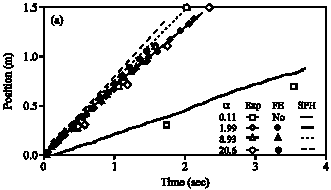
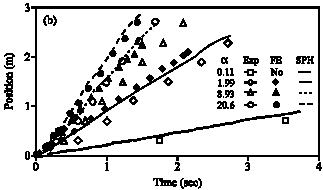
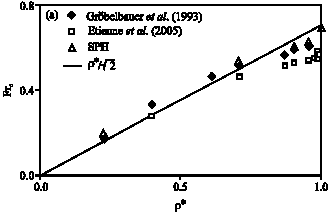
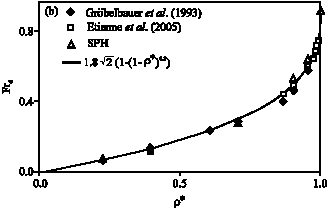
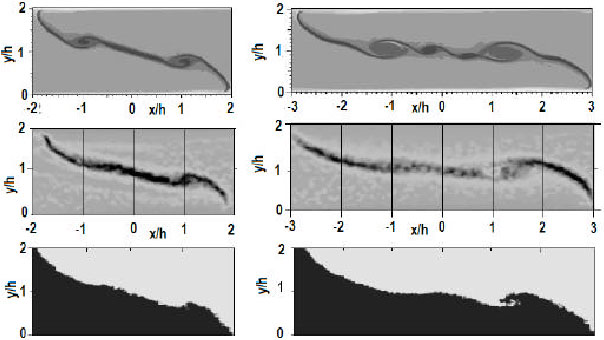
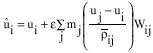Research Article
Modeling Two-Phase Flows Using SPH Method
Department of Civil Engineering, Tarbiat Modares University, Tehran, Iran
M. Shafieefar
Department of Civil Engineering, Tarbiat Modares University, Tehran, Iran
J.J. Monaghan
School of Mathematical Sciences, Monash University, Clayton, Australia
S.A.A. Salehi Neyshaboori
Department of Civil Engineering, Tarbiat Modares University, Tehran, Iran