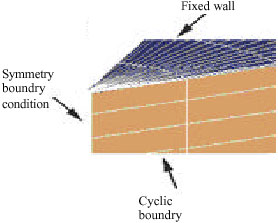
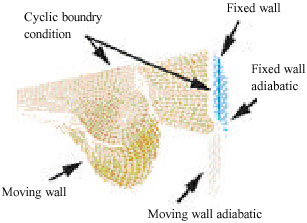
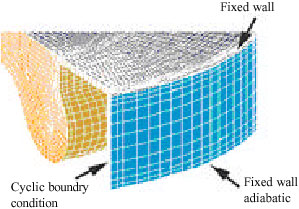
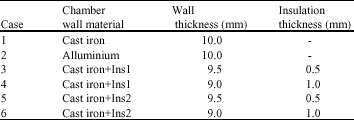
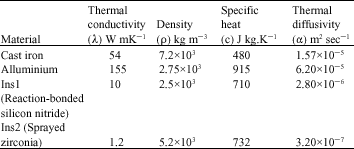
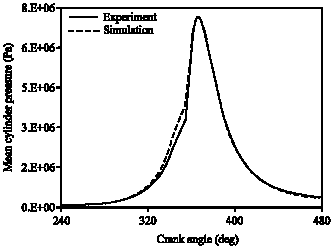
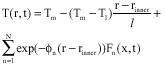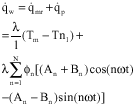Research Article
Multidimensional Combustion Simulation and Analytical Solution of Wall Heat Conduction in DI Diesel Engine
Department of Mechanical Engineering, University of Tabriz, Tabriz, Iran
F. Talati
Department of Mechanical Engineering, University of Tabriz, Tabriz, Iran
A. Ghasemi
Department of Mechanical Engineering, University of Tabriz, Tabriz, Iran
S. Sohrabi
Department of Mechanical Engineering, University of Tabriz, Tabriz, Iran