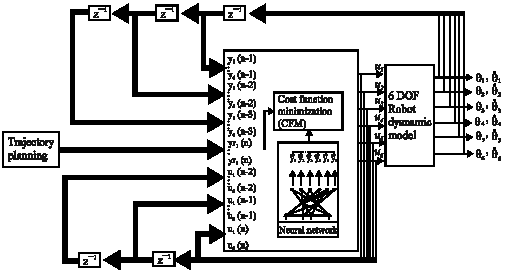
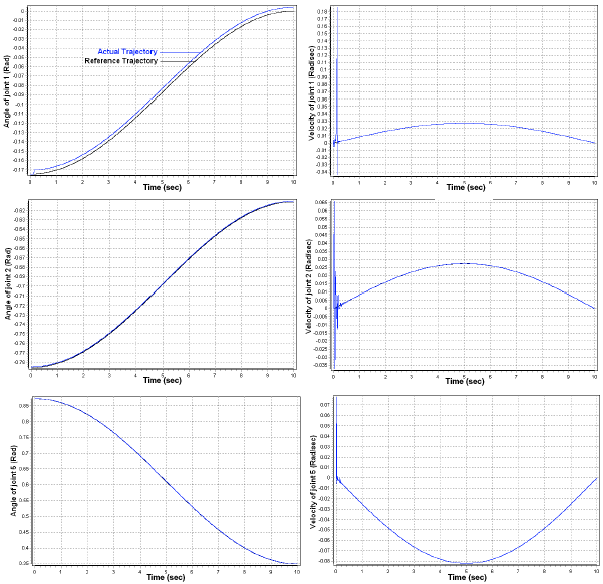
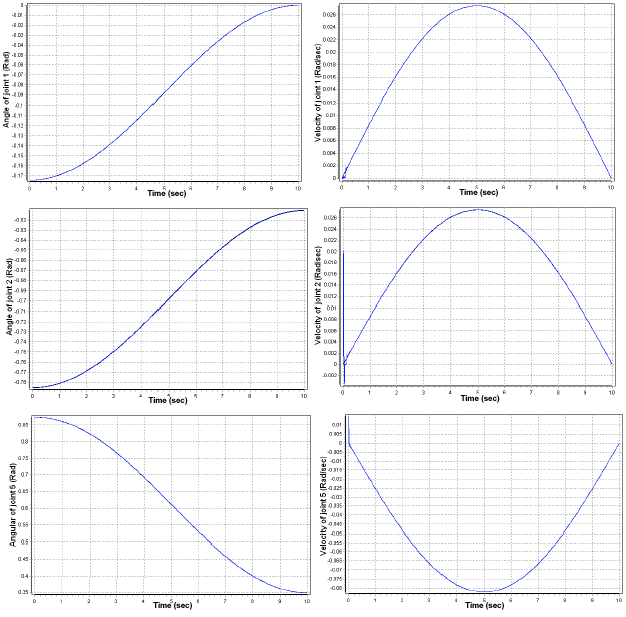
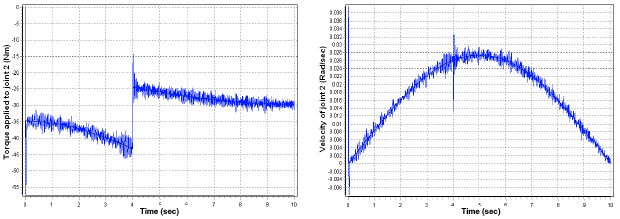
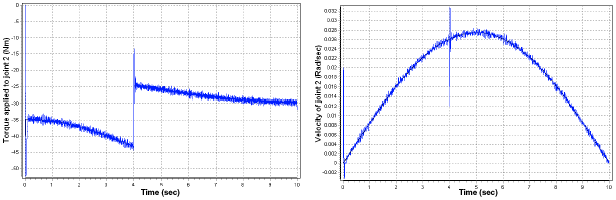
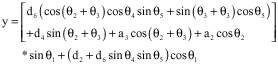Research Article
Nonlinear Generalized Predictive Controller Based on Artificial Neural Network for Robot Control
Department of Electric-Electronic Engineering, Sakarya University, 54187 Adapazari, Turkey
N. Yumusak
Department of Computer Engineering, Sakarya University, 54187 Adapazari, Turkey