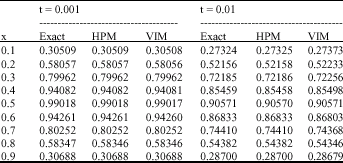
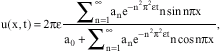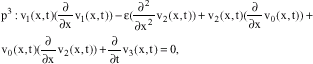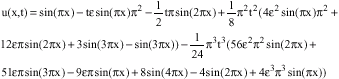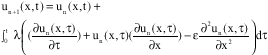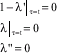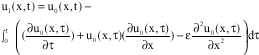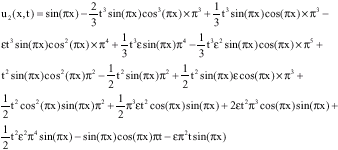Research Article
Variational Iteration Method and Homotopy-Perturbation Method for Solving Burgers Equation in Fluid Dynamics
Department of Civil Engineering, University of Mazandaran, P.O. Box 484, Babol, Iran
A. Tahmasebi Poor
Department of Civil Engineering, University of Mazandaran, P.O. Box 484, Babol, Iran
M. Omidvar
Department of Civil Engineering, University of Mazandaran, P.O. Box 484, Babol, Iran